
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометричне розв’язання задач лінійного програмування у випадку, коли число змінних більше двох.Геометричний метод розв’язування задач лінійного програмування іноді можна застосовувати і у випадку, коли число змінних більше двох. Наприклад, якщо задача задана в канонічній формі і система обмежень дозволяє виразити всі змінні через які-небудь дві з них. Тоді підставляючи ці вирази в цільову функцію, одержимо функцію двох змінних. Виключаючи виражені змінні в обмеженнях, переходимо від обмежень-рівностей до обмежень-нерівностей виду (2). Приклад 4. Знайти найбільше значення функції
Розв’язання. Виражаємо з обмежень задачі всі змінні через
Тепер з другого рівняння можна визначити
Нарешті, вирази для
Таким чином, ми одержали задачу для функції двох змінних: знайти найбільше значення функції
Побудуємо тепер многокутник
Отже, найбільше значення функції
Відповідь:
Приклад 5. Знайти мінімум цільової функції 
Тепер задачу можна розв’язати графічно. Побудуємо многокутник допустимих планів Легко бачити, що цільова функція досягає мінімуму в точці
Відповідь: |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 196. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 при обмеженнях:
при обмеженнях:
 і
і  . Спочатку з третього рівняння системи знаходимо
. Спочатку з третього рівняння системи знаходимо  :
: 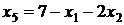 . Підставивши цей вираз в перше і друге рівняння, одержимо:
. Підставивши цей вираз в перше і друге рівняння, одержимо:
 :
:  . Підставивши вираз
. Підставивши вираз  , звідки
, звідки  . За умовою задачі змінні
. За умовою задачі змінні  ,
, 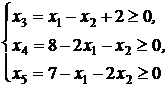 або
або 
 .
. при таких обмеженнях:
при таких обмеженнях:
 , обумовлений останньою системою обмежень, і пряму
, обумовлений останньою системою обмежень, і пряму  , задану рівнянням
, задану рівнянням 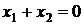 :
: Паралельним переносом прямої
Паралельним переносом прямої  , визначимо точку A многокутника
, визначимо точку A многокутника  (
( 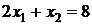 ) і
) і  (
(  ):
): .
. в області, зумовленої обмеженнями задачі, досягається при
в області, зумовленої обмеженнями задачі, досягається при 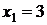 ,
,  і воно дорівнює
і воно дорівнює  . Знайдемо тепер значення змінних
. Знайдемо тепер значення змінних  :
: ,
,  ,
,  .
.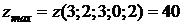 .
. при таких обмеженнях:
при таких обмеженнях: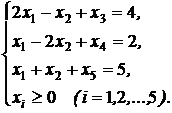
 Розв’язання. Виходячи з вигляду цільової функції, можна перейти від початкової системи обмежень-рівностей до системи обмежень-нерівностей:
Розв’язання. Виходячи з вигляду цільової функції, можна перейти від початкової системи обмежень-рівностей до системи обмежень-нерівностей:
 .
.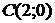 :
: .
. .
.