
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Электромагнитные волны в вакууме, их свойства и основные характеристики. Поляризация электромагнитных волн.Положим в дифференциальных уравнениях Максвелла плотность зарядов r и плотность токов Из уравнений (2) и (4) следует, что электрическое и магнитное поля соленоидальны, т.е. линии векторов Покажем, что из уравнений Максвелла следует вывод о распространении электромагнитной волны. Продифференцируем по времени обе части уравнения (3): Подставим в (5) (1) и учтем, что Выполняя аналогичные преобразования с двумя другими уравнениями Максвелла, получим волновое уравнение для вектора Решение волновых уравнений (6) и (7) записывается в виде плоских волн  Из уравнений Максвелла можно также получить следующие свойства электромагнитных волн.
2. В электромагнитной волне
Характеристикой электромагнитной волны является плотность потока энергии (вектор Пойтинга)
В заданном объеме V электромагнитная волна обладает энергией: Формулы (8) с условием (9) описывают плоские волны напряженности и индукции, распространяющиеся в пространстве со скоростью с. Важное значение имеет частный случай плоских волн – плоские монохроматические волны: В общем случае электромагнитная волна может быть представлена суперпозицией плоских монохроматических волн всевозможных частот, амплитуд и направлений. Частными решениями уравнений (6) и (7) являются функции вида Электромагнитная волна с векторами Плоскость, проходящая через направление распространения волны Если положение плоскости поляризации остается неизменным, то волна будет плоско поляризованной. Для плоскополяризованной волны может быть несколько состояний поляризации: эллиптическая, круговая, линейная. Так, уравнения (12) описывают линейно поляризованную волну, т.к. конец вектора |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 503. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
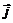 равными нулю. Тогда уравнения будут описывать электромагнитное поле в вакууме:
равными нулю. Тогда уравнения будут описывать электромагнитное поле в вакууме: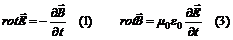
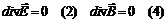
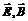 замкнуты. Источников линий электрического поля нет, и они охватывают силовые линии магнитного поля. Магнитное поле соленоидально и силовые линии магнитного поля охватывают силовые линии электрического поля. Обе компоненты электромагнитного поля
замкнуты. Источников линий электрического поля нет, и они охватывают силовые линии магнитного поля. Магнитное поле соленоидально и силовые линии магнитного поля охватывают силовые линии электрического поля. Обе компоненты электромагнитного поля 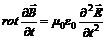 (5)
(5)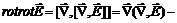
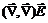 =
= 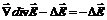 , тогда
, тогда 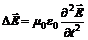 Величина
Величина 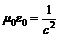 , где с – скорость распространения электромагнитной волны.
, где с – скорость распространения электромагнитной волны.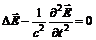 (6)
(6)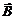 :
: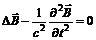 (7)
(7)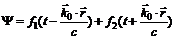 , единичный вектор
, единичный вектор 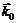 указывает направление распространения волны, f1 – волна, распространяющаяся в направлении вектора
указывает направление распространения волны, f1 – волна, распространяющаяся в направлении вектора 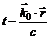 :
: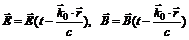 (8)
(8)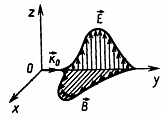 1. Электромагнитные волны в вакууме поперечные, т.е.
1. Электромагнитные волны в вакууме поперечные, т.е. 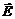 и
и 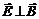 . Модули векторов связаны соотношением
. Модули векторов связаны соотношением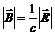 . (9)
. (9)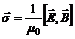 . (10)
. (10)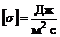 . Модуль вектора Пойтинга равен энергии, переносимой за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения электромагнитной волны.
. Модуль вектора Пойтинга равен энергии, переносимой за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения электромагнитной волны.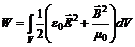 (11)
(11)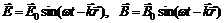 , где
, где 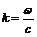 ,
, 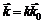 . (12)
. (12)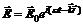 и
и 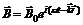
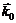 и вектор
и вектор