
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Электростатическое поле в вакууме, его потенциальность. Потенциал и напряженность поля системы зарядов в дипольном приближении.Всякий электрический заряд определенным образом изменяет свойства окружающего его пространства – создает электрическое поле. Это поле проявляет себя в том, что помещенный в какую-либо его точку другой, "пробный", заряд испытывает действие силы. Опыт показывает, что сила Это утверждение называют принципом суперпозиции электрических полей. Уравнения, описывающие электростатическое поле в вакууме, имеют вид:
Для электростатического поля, кроме дифференциальных уравнений (1) справедливо интегральное соотношение, именуемое теоремой Гаусса. Теорема Гаусса. Поток вектора
Эта теорема применяется для расчета полей при симметричном распределении зарядов. Например в случае равномерно заряженной бесконечной нити, бесконечного цилиндра, сферы, шара. Векторное поле, ротор которого равен нулю, называется потенциальным. Электростатическое поле является потенциальным, т.к.  Линии напряженности электростатического поля начинаются на положительных зарядах и оканчиваются на отрицательных. В силу (2) в электростатическом поле работа сил поля при перемещении заряда из одной точки в другую не зависит от пути, по которому производится это перемещение, а зависит только от начальной и конечной точек пути. Рассмотрим движение из точки А в точку В по пути Г1 и пути Г2. Работа сил поля при перемещении единичного положительного заряда по замкнутому контуру, состоящему из путей Г1 и Г2 равна
Так как ротор градиента всегда равен нулю, то общим решением уравнения (2) является Знак минус возник исторически, никакого принципиального значения он не имеет. Но благодаря этому знаку вектор напряженности направлен в сторону уменьшения потенциала. Электростатический потенциал j равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда. Непосредственный физический смысл имеет разность потенциалов двух точек поля, которая определяет работу электростатического поля по переносу заряда из одной точки в другую. Электростатическое поле описывают либо уравнениями (1), либо уравнением Пуассона для скалярного потенциала j: Решение уравнения (4) имеет вид:
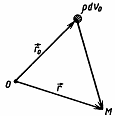
Практическое применение формулы (5) возможно лишь для случая простой зависимости плотности заряда r от расстояния. В общем случае вычисление интеграла оказывается достаточно сложной задачей. Вычисление интеграла (5) допускает приближенное решение лишь для случая, когда рассчитывается потенциал поля на большом расстоянии от зарядов. Тогда потенциал (5) допускает разложение в ряд, причем основной вклад в разложение дают первые два члена:
Q – общий заряд системы, (7) определяет напряженность поля, созданного электронейтральной системой зарядов на большом расстоянии от неё. Энергия электростатического поля с напряженностью |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 360. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
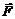 , действующая на неподвижный заряд Q, всегда может быть представлена как
, действующая на неподвижный заряд Q, всегда может быть представлена как 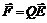 , где
, где 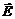 – напряженность электрического поля. Напряженность поля выражается в вольтах на метр (В/м). Опытные факты говорят о том, что напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждые из зарядов в отдельности:
– напряженность электрического поля. Напряженность поля выражается в вольтах на метр (В/м). Опытные факты говорят о том, что напряженность поля системы точечных неподвижных зарядов равна векторной сумме напряженностей полей, которые создавали бы каждые из зарядов в отдельности: 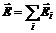 .
.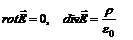 (1)
(1)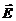 сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов внутри этой поверхности, деленной на e0.
сквозь произвольную замкнутую поверхность S равен алгебраической сумме зарядов внутри этой поверхности, деленной на e0.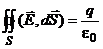
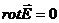 . (2)
. (2)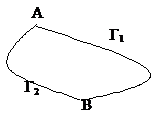 Докажем это.
Докажем это.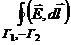 по теореме Стокса этот интеграл равен
по теореме Стокса этот интеграл равен 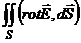 , где S – поверхность, натянутая на рассматриваемый контур. Но в силу (2)
, где S – поверхность, натянутая на рассматриваемый контур. Но в силу (2) 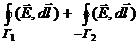 =
= 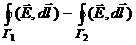 =0, то есть,
=0, то есть,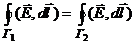 .
.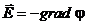 (3).
(3).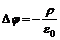 (4)
(4)
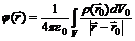 (5)
(5)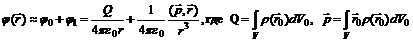 (6)
(6)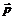 – дипольный момент системы. На практике особое значение имеют электронейтральные системы. Это атомы и молекулы в нормальном состоянии, незаряженные тела. Тогда в (6) Q = 0, и потенциал поля определяется дипольным приближением
– дипольный момент системы. На практике особое значение имеют электронейтральные системы. Это атомы и молекулы в нормальном состоянии, незаряженные тела. Тогда в (6) Q = 0, и потенциал поля определяется дипольным приближением 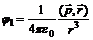 . Расчет напряженности электростатического поля по формуле (3) дает значение
. Расчет напряженности электростатического поля по формуле (3) дает значение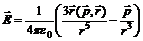 . (7)
. (7)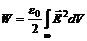 . Интегрирование производится по всему пространству, чтобы учесть все поле, созданное зарядами.
. Интегрирование производится по всему пространству, чтобы учесть все поле, созданное зарядами.