
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Постоянное магнитное поле, его вихревой характер.Постоянные магнитные поля порождаются постоянными токами. Постоянное магнитное поле в вакууме описывается следующими уравнениями:
При симметричном распределении токов в пространстве применяют интегральную форму записи первого уравнения (1): Циркуляция вектора Поле Для магнитного поля справедлив принцип суперпозиции: магнитное поле, создаваемое несколькими движущимися зарядами или токами, равно векторной сумме полей, создаваемых каждым зарядом или током в отдельности Для характеристики магнитных полей используется векторный потенциал причем,  Решение (3) имеет вид:
Интеграл (5) в общем случае при произвольном распределении токов в пространстве вычислить достаточно сложно. Приближенное решение получают для случая расчета векторного потенциала на больших расстояниях от системы токов. В этом случае решение интеграла (5) в дипольном приближении имеет вид: где Отметим, что (7) аналогична формуле для напряженности электростатического поля электронейтральной системы зарядов в дипольном приближении. Энергия магнитостатического поля с индукцией Интегрирование производят по всему пространству, чтобы учесть все поле, созданное зарядами. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 363. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 . (1)
. (1)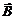 – индукция магнитного поля, [В]= Тл,
– индукция магнитного поля, [В]= Тл,  плотность токов проводимости ,
плотность токов проводимости , 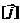 =A/м2, Так как
=A/м2, Так как  , то магнитное поле называется вихревым.
, то магнитное поле называется вихревым. . (2)
. (2) выражает тот факт, что магнитное поле не имеет источников в виде свободных магнитных зарядов.
выражает тот факт, что магнитное поле не имеет источников в виде свободных магнитных зарядов. .
.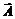 , удовлетворяющий уравнению
, удовлетворяющий уравнению , (3)
, (3) . (4)
. (4)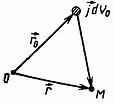
 (5)
(5) (6)
(6) – магнитный момент системы токов
– магнитный момент системы токов  . Подставив (6) в (4), получим выражение для индукции магнитного поля токов на большом расстоянии от них:
. Подставив (6) в (4), получим выражение для индукции магнитного поля токов на большом расстоянии от них: (7)
(7) .
.