
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Уравнения Максвелла для системы зарядов в вакууме, их физический смысл.Система уравнений Максвелла – основа электродинамики и является обобщением экспериментальных данных. Уравнения Максвелла записывают в интегральной и дифференциальной форме. Дифференциальная форма Интегральная форма
где Уравнения (1) – (4) устанавливают связь между векторами электромагнитного поля, плотностью зарядов и плотностью токов в любой точке пространства в любой момент времени. Дифференциальная форма уравнений позволяет рассчитать электромагнитное поле по распределению зарядов и токов в пространстве. Но это достаточно сложная задача с точки зрения математики, поэтому часто при решении конкретных задач используют интегральную форму. Кроме того, интегральная форма нагляднее физически. Для примера рассмотрим дифференциальное уравнение (4). Выделим в пространстве некоторый объем V, ограниченный поверхностью S. Пусть внутри объема находятся заряды, распределенные с плотностью r. Проинтегрируем данное уравнение по объему V: Применим к левой части (5) теорему Остроградского: Интеграл  Для наглядности поле вектора Физический смысл уравнений (4). Источниками электрического поля являются электрические заряды. Поток вектора напряженности электрического поля через замкнутую поверхность S определяется суммарным электрическим зарядом, находящимся внутри данной поверхности. С уравнениями (4) связан закон Кулона. Уравнения (1) связаны с законом Фарадея для электромагнитной индукции. Физический смысл уравнений: вихревое электрическое поле порождается переменным магнитным полем. Величина Уравнения (2) показывают, что отсутствуют магнитные заряды и силовые линии магнитного поля всегда замкнуты. Сколько силовых линий выходит из объема V, столько и заходит в этот объем. Можно также сказать, что силовые линии магнитного поля либо замкнуты, либо приходят из бесконечности и уходят на бесконечность. В уравнениях (3) Уравнения Максвелла (1)-(4) применимы для исследования потоков элементарных частиц или ионов в пустоте (например, плазма, ионные пучки). В ряде случаев, когда окружающие тела не влияют на электромагнитное поле, данные уравнения применяют и для расчета полей в веществе. Например, поле малых заряженных тел в воздухе рассчитывается как поле точечных зарядов в вакууме, магнитное поле линейного проводника с током – как поле тока в вакууме. Из уравнений Максвелла выводится ряд фундаментальных законов и следствий, подтверждаемых экспериментом, например, закон сохранения заряда, закон сохранения энергии и импульса электромагнитного поля и т.д. Покажем, как закон сохранения заряда получается из уравнений Максвелла. Вычислим дивергенцию от обеих частей уравнения (3), при этом используем свойство цикличности перестановок в смешанном произведении: Подставив в (7) (4), получим закон сохранения заряда в дифференциальной форме: |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 366. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |


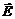 – напряженность электрического поля,
– напряженность электрического поля, 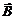 – вектор индукции магнитного поля,
– вектор индукции магнитного поля, 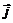 – плотность токов проводимости,
– плотность токов проводимости,  – плотность токов смещения, r– плотность зарядов. В уравнения входят константы m0 =4p×10–7В×с/(А×м) – магнитная постоянная, e0= 8,85×10–12 Ф/×м – электрическая постоянная.
– плотность токов смещения, r– плотность зарядов. В уравнения входят константы m0 =4p×10–7В×с/(А×м) – магнитная постоянная, e0= 8,85×10–12 Ф/×м – электрическая постоянная. (5)
(5) (6)
(6)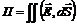 определяет поток вектора напряженности
определяет поток вектора напряженности  Соотношение (6) называют теоремой Гаусса.
Соотношение (6) называют теоремой Гаусса.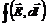 определяет э.д.с индукции, а
определяет э.д.с индукции, а  – поток вектора магнитной индукции через поверхность S. Э.д.с. индукции, возникающая в замкнутом проводнике L, определяется изменяющимся магнитны потоком, пронизывающим контур проводника.
– поток вектора магнитной индукции через поверхность S. Э.д.с. индукции, возникающая в замкнутом проводнике L, определяется изменяющимся магнитны потоком, пронизывающим контур проводника.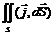 и
и  – токи проводимости и токи смещения,
– токи проводимости и токи смещения,  , тогда
, тогда  или
или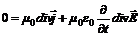 (7)
(7)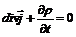 (8).
(8).