
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функция Лагранжа одномерного движения. Общее решение задачи о движении в постоянном потенциале. Период финитного движения. Математический маятник.Одномерным называется движение системы с одной степенью свободы. Наиболее общий вид функции Лагранжа для такого движения в постоянных внешних условиях: где m(q) – некоторая функция обобщенной координаты q. В частности, если q – декартова координата х, то Закон движения такой системы может быть найден в общем виде когда потенциальная энергия не зависит от времени. В этом случае Из данного уравнения получим: Решая уравнение (4) находят связь между х и t, т.е. находят уравнение движения x(t). Так как кинетическая энергия положительная величина, то полная энергия всегда больше потенциальной. Т.е. движение возможно только в том Проведем на графике прямую, соответствующую заданному значению полной энергии. Условию E> U(x) отвечает движение в области АВ или в области справа от С. Точки, в которых E = U(x) определяют границы движения и называются точками остановки. Движение в области, ограниченной двумя точками, называется финитным. Если область движения не ограничена или ограничена с одной стороны, то такое движение называется инфинитным. На рисунке АВ – область финитного движения, область справа от точки С – инфинитного.  Одномерное финитное движение является колебанием. На рисунке тело движется в потенциальной яме АВ между точками х1и х2. Период колебания равен удвоенному времени прохождения отрезка [x1, x2]. Как следует из (4): Если использовать запись функции Лагранжа в виде (1), то формула для периода колебания примет наиболее общий вид: Рассмотрим в качестве примера движение математического маятника. Тело массы m, соединенное жестким невесомым стержнем длины l с неподвижной Обобщенной координатой маятника выберем угол j между вертикалью и стержнем. Тогда декартовы координаты связаны с j следующим образом: Углы j1 и j2 находят из условия E=U. Если полная энергия Е будет больше mglcosj, то уравнение E=U не будет иметь решений и движение маятника будет представлять собой вращение. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 442. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
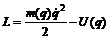 , (1)
, (1)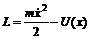 . (2)
. (2)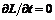 и сохраняется энергия системы:
и сохраняется энергия системы: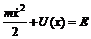 . (3)
. (3)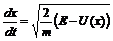 , откуда
, откуда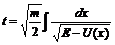 . (4)
. (4)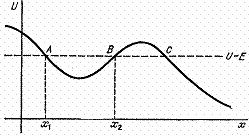 случае, когда E> U(x). Пусть график потенциальной энергии имеет вид, изображенный на рисунке.
случае, когда E> U(x). Пусть график потенциальной энергии имеет вид, изображенный на рисунке.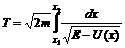 . (5)
. (5)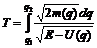 (6)
(6)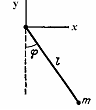 точкой подвеса движется в вертикальной плоскости под действием силы тяжести.
точкой подвеса движется в вертикальной плоскости под действием силы тяжести.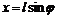 ,
, 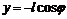 . Отсюда
. Отсюда 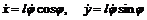 ,
, 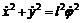
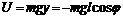 . Функция Лагранжа математического маятника имеет вид:
. Функция Лагранжа математического маятника имеет вид: 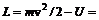
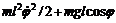 . Сравнивая данное соотношение с формулой (1), получим, что m(q)= ml2. Тогда период колебания математического маятника в соответствии с формулой (6):
. Сравнивая данное соотношение с формулой (1), получим, что m(q)= ml2. Тогда период колебания математического маятника в соответствии с формулой (6): 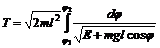 (7)
(7)