
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Лагранжев формализм. Функция Лагранжа, уравнения Лагранжа, обобщенные импульс, сила, энергия. Принцип наименьшего действия.Стр 1 из 26Следующая ⇒ ЕЛАБУЖСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ (ГОУ ВПО ЕГПУ)
Основы теоретической физики Конспект обзорных лекций
Елабуга 2008 УДК 530.1 ББК 22.31 Х – 30
Печатается по решению редакционно-издательского совета Елабужского государственного педагогического университета (протокол № 22 от 24 января 2008 г.)
Рецензенты:
Ф.М. САБИРОВА, к. ф.-м. н, доцент кафедры общей физики ЕГПУ А.В. Костин, к. ф.-м. н, заведующий кафедрой общенаучных дисциплин КГТУ им. А.Н. Туполева
Основы теоретической физики.Конспект обзорных лекций./Автор-сост. И.И. Хвалченко. – Елабуга: ЕГПУ, 2008. – 72 с.
Учебное пособие для студентов физико-математического факультета педагогического университета.
Елабужский государственный педагогический университет Ó Введение В предлагаемом пособии рассмотрены избранные вопросы курса "Основы теоретической физики", изучаемого на физико-математических факультетах педагогических вузов. По каждому вопросу даны определения основных понятий, изложены физические законы и применяемый математический аппарат. Рассмотрено приложение математического аппарата к решению задач теоретического и практического назначения. Предлагаемое пособие составлено в соответствии с государственными образовательными стандартами высшего профессионального образования и может быть использовано как справочное руководство при подготовке к государственному экзамену по физике.
Лагранжев формализм. Функция Лагранжа, уравнения Лагранжа, обобщенные импульс, сила, энергия. Принцип наименьшего действия.  Для задания положения материальной точки в любой момент времени используется радиус вектор Таким образом, основная задача механики сводится к двукратному интегрированию уравнения (1). Но непосредственное интегрирование (1) не всегда является удобным способом решения. Это связано с тем, что если система состоит из N тел, то (1) будет представлять собой систему из 3N дифференциальных уравнений. Если, кроме этого, система обладает определенной симметрией, то лучше использовать вместо декартовой системы координат другую, соответствующую симметрии данной системы. Поэтому в ряде задач механики используется лагранжев формализм, при котором механической системе сопоставляется функция обобщенных координат, обобщенных скоростей и времени: Покажем, как от уравнений Ньютона можно перейти к лагранжеву формализму. Рассмотрим систему, состоящую из N взаимодействующих частиц с массами m(1), m(2),…: Введем следующие обозначения: m1 = m2 =m3 =m(1)– масса 1-ой частицы, m4 = m5 =m6 =m(2) масса 2-ой частицы, ..., х1– координата х 1-ой частицы, х2– координата у 1-ой частицы, х3– координата z 1-ой частицы, x4, x5, x6 – координаты x, y, z 2-ой частицы, …, F1, F2, F3 – проекции на оси x,y,z силы, действующей на 1-ю частицу, F4, F5, F6 – проекции на оси x,y,z силы, действующей на 2-ю частицу и т.д. Если на частицы действуют потенциальные силы, то они могут быть выражены следующим образом: где Пусть часть сил, действующих на систему частиц потенциальна, а часть – не потенциальна, тогда уравнения движения частиц системы:
Определим для данной системы функцию Лагранжа как разность кинетической и потенциальной энергии: Продифференцировав по времени частную производную от L по Продифференцировав L по хk, получим k-ю компоненту потенциальной силы: Таким образом, мы приходим к уравнениям: которые называются уравнения Лагранжа. Для систем, в которых действуют только потенциальные силы, уравнения Лагранжа имеют вид: Мы получили уравнения Лагранжа (6) в декартовых координатах для системы частиц без связей. Если на систему частиц наложены связи, ограничивающие движение, то удобно ввести обобщенные координаты qk и обобщенные скорости Функция Лагранжа Из выражения для функции Лагранжа (4) следует, что производная называют обобщенным импульсом, а величину - обобщенной силой. Через функцию Лагранжа выражается также полная энергия системы. (10) является самым общим выражением энергии системы и остается пригодным даже в том случае, когда полная энергия не может быть представлена в виде суммы кинетической и потенциальной энергией. В основу механики вместо законов Ньютона можно положить принцип наименьшего действия или принцип Гамильтона. Действием S за промежуток времени [t1, t2] называется интеграл Положение системы характеризуется координатами qk(t). Согласно принципу наименьшего действия система на временном интервале [t1, t2] всегда движется так, что ее действие S принимает наименьшее возможное значение. Размерность действия равна Дж×с. Такую же размерность имеет постоянная Планка, которую называют также квантом действия. Принцип Гамильтона представляет собой наиболее общую формулировку закона движения механических систем. Он может быть применен не только к механическим системам, но и к упругим средам, электромагнитным полям и т.п. |
||
|
Последнее изменение этой страницы: 2018-05-29; просмотров: 378. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
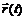 . Определение зависимости
. Определение зависимости 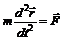 . (1)
. (1)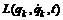 , которую называют функцией Лагранжа. Обобщенными координатами qk называют любые величины, с помощью которых может быть задано положение системы в пространстве. Обобщенными скоростями
, которую называют функцией Лагранжа. Обобщенными координатами qk называют любые величины, с помощью которых может быть задано положение системы в пространстве. Обобщенными скоростями 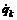 называют производные обобщенных координат по времени. Записав для системы функцию Лагранжа, можно решить основную задачи механики с помощью уравнений Лагранжа, которые заменяют уравнения Ньютона. Использование уравнений Лагранжа удобно тем, что количество этих уравнений равно числу степеней свободы системы. В случае, когда на систему наложены связи, число этих уравнений будет меньше 3N. Под связями понимают любые ограничения, наложенные на систему. На практике очень важен и часто встречается случай, когда связь может быть описана с помощью уравнения, связывающего координаты точек системы:
называют производные обобщенных координат по времени. Записав для системы функцию Лагранжа, можно решить основную задачи механики с помощью уравнений Лагранжа, которые заменяют уравнения Ньютона. Использование уравнений Лагранжа удобно тем, что количество этих уравнений равно числу степеней свободы системы. В случае, когда на систему наложены связи, число этих уравнений будет меньше 3N. Под связями понимают любые ограничения, наложенные на систему. На практике очень важен и часто встречается случай, когда связь может быть описана с помощью уравнения, связывающего координаты точек системы: 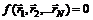 . Такая связь называется голономной, примером голономной связи может служить жесткий невесомый стержень, связывающий две частицы.
. Такая связь называется голономной, примером голономной связи может служить жесткий невесомый стержень, связывающий две частицы.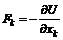 , (2)
, (2)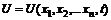 – функция координат и времени, называемая потенциалом. Если в функцию U время явно не входит, то она называется потенциальной энергией системы.
– функция координат и времени, называемая потенциалом. Если в функцию U время явно не входит, то она называется потенциальной энергией системы.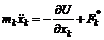
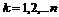 (3)
(3)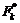 – компоненты непотенциальных сил. Число n уравнений, входящих в (3), равно утроенному числу частиц системы (
– компоненты непотенциальных сил. Число n уравнений, входящих в (3), равно утроенному числу частиц системы ( 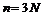 ).
). 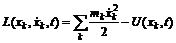 . (4)
. (4)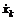 , получим левую часть уравнения (3):
, получим левую часть уравнения (3):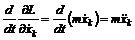 .
.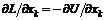 .
.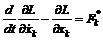 ,
, 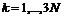 (5)
(5)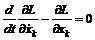 . (6)
. (6)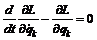 (7)
(7) 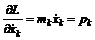 – проекция импульса соответствующей частицы на одну из координатных осей, а
– проекция импульса соответствующей частицы на одну из координатных осей, а 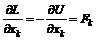 – проекция потенциальной силы, действующая на частицу. Аналогично при использовании обобщенных координат величину
– проекция потенциальной силы, действующая на частицу. Аналогично при использовании обобщенных координат величину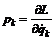 (8)
(8)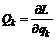 (9)
(9)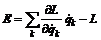 (10)
(10)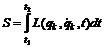 (12)
(12)