
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пространственно - усилительное звено
где: Е1 - заданное число (общий коэффициент усиления); x, y – пространственные координаты;
n1 – весовой коэффициент (n1 ≥ 1). Используя обобщенную координату, передаточная функция пространственно-усилительного звена может быть записана в виде
где G - обобщенная координата [1,4].
Идеальное пространственно - дифференцирующее звено Передаточная функция такого звена имеет вид:
где: Е2 – заданный коэффициент; n2 – весовой коэффициент (n2 ≥ 1). Используя обобщенную координату, передаточная функция идеального пространственно - дифференцирущего звена может быть записана в виде
Динамические характеристики звена в области S1 =jω1 могут быть записаны в виде:
На рис.1.1. частотные характеристики идеального пространственно-дифференцирующего звена.
Рис. 1.1. Частотные поверхности Пространственно-форсирующее звено Передаточная функция этого звена имеет вид:
где: E3 – заданное число; n3 – весовой коэффициент (n3 ≥ 1). С учетом обобщенной координаты звено записывается в виде
Динамические характеристики пространственно-форсирующего звена в области s1 =jω1 могут быть записаны в виде:
На рис. 1.2 приведены частотные поверхности пространственно-форсирующего звена.
Рис. 1.2. Частотные поверхности пространственно-форсирующего звена Идеальное пространственно-интегрирующее звено Передаточная функция идеального пространственно-интегрирующего звена имеет вид:
где E4 – заданное число; n4 – весовой коэффициент (n4 ≥ 1). Передаточная функция звена, записанная с использованием обобщенной координаты (G), имеет вид: 
Динамические характеристики идеального пространственно-интегрирующего звена в области s1 =jω1 могут быть записаны в виде:
Преобразуя, получим
На рис.1.3 приведены частотные поверхности пространственно-интегрирующего звена.
Рис. 1.3. Частотные поверхности пространственно-интегрирующего звена
Пространственно - изодромное звено Передаточная функция пространственно-изодромного звена имеет вид:
где E5 – заданное число; n5 – весовой коэффициент (n5 ≥ 1).
На рис.1.4 приведены частотные поверхности пространственно-изодромного звена.
Рис.1.4. Частотные поверхности пространственно - изодромного звена
Распределенный высокоточный регулятор Передаточная функция РВР , сформированная из распределенных звеньев (пространственно – усилительного, идеального пространственно-интегрирующего и идеального пространственно – дифференцирующего) имеет вид:
Передаточная функция РВР, записанная с использованием обобщенной координаты, может быть представлена в виде следующего соотношения:
Динамические характеристики РВР в области s1 =jω1 могут быть записаны в виде:
На рис. 1.5 приведены частотные поверхности РВР
Рис. 1.5. Частотные поверхности РВР
ГЛАВА 2. МЕТОДИКА СИТЕЗА РАСПРЕДЕЛЕННЫХ СИСТЕМ УПРАВЛЕНИЯ В главе приводятся основы методики синтеза сосредоточенных систем с использованием качественной теории, а так же рассматриваются особенности систем с распределенными параметрами и методика синтеза распределенных регуляторов. 2.1. Методика синтеза сосредоточенных систем
Методику синтеза сосредоточенных систем управления рассмотрим на примере определения коэффициента усиления регулятора для системы управления сосредоточенным объектом, передаточная функция которого задана в виде:
Методика синтеза сосредоточенных систем управления распадается на следующие этапы: 1. Динамические характеристики объекта (2.1) (комплексный передаточный коэффициент) в области s1 =jω1 могут быть записаны в виде:
2. Используя соотношение (2.2) построим модифицированный годограф (см.рис. 2.1). 3. В соответствии с критерием устойчивости Найквиста [13,14], определим статический коэффициент усиления регулятора К= -1/(-0.05)=20 (см. рис. 2.1).
Рис.2.1. Модифицированный годограф рассматриваемого объекта
Моделируя работу замкнутой системы, получены графики переходного процесса, приведенные на рис. 2.2.
Рис. 2.2. Результаты моделирования замкнутой системы управления
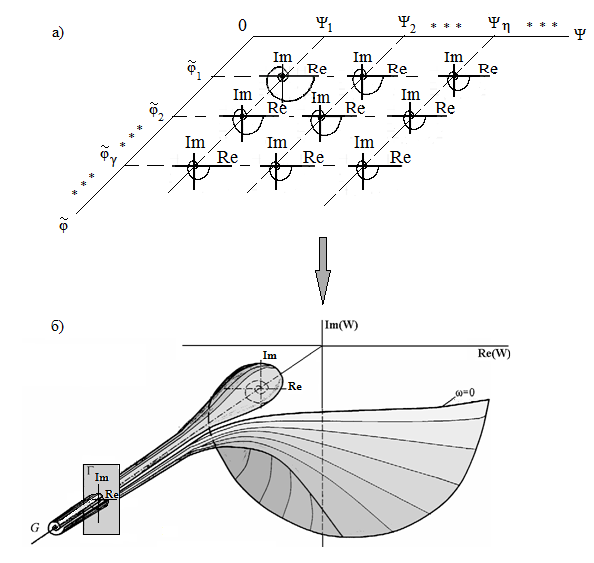
Аналогичным образом могут быть синтезированы и другие законы управления. 2.2. Особенности систем с распределенными параметрами При исследовании систем с распределенными параметрами в [1-4] введено понятие пространственных мод ̶ собственных вектор - функций операторов объектов. Собственное движение таких пространственных мод описывается бесконечными дифференциальными уравнениями. Преобразование по Лапласу таких уравнений приводит к бесконечным полиномам (к бесконечному числу корней по каждой пространственной моде). При этом число собственных вектор – функций оператора объекта (пространственных мод) так же бесконечно. Для описания динамических характеристик распределенного объекта управления в [1,4] введена обобщенная координата G. Она позволяет бесконечную совокупность годографов (см. рис. 2.3, а), описывающих динамические характеристики по каждой пространственной моде, свести к поверхности - пространственному годографу (см. рис.2.3, б).
Рис.2.3. Пространственный годограф
Частотная процедура синтеза [1-4] разработана с использованием пространственного годографа (рис. 2.3). Под качественным распределением мод для систем с распределенными параметрами понимается расположение мод в цилиндре радиуса r больше нуля, с центром в точке (Re=β,Im=0), причем значении β+r должно быть меньше нуля. То есть данный круг должен лежать в левой полуплоскости комплексной плоскости корней, где параметр β определяет среднюю скорость сходимости процессов к положению равновесия, а параметр r– определяет отклонения траекторий движения от средних значений (см. рис.2.4,а), где G – обобщенная координата, с помощью которой учитывается бесконечная совокупность пространственных мод
Рис.2.4. Модифицированный пространственный годограф
Критерий Найквиста может быть применен и для анализа качественного расположение мод в замкнутой распределенной системе. Если разомкнутый контур по каждой пространственной моде качественно экспоненциально устойчив с параметрами β и r, то амплитудно-фазо-частотная характеристика передаточной функции разомкнутого контура в области s1 =jω1 не должна охватывать точку (Re=-1, Im=0) комплексной плоскости. Динамические характеристики разомкнутой распределенной системы, описывающие характеристики по каждой пространственной моде, можно свести к поверхности – модифицированному пространственному годографу (см. рис.2.4, б). В этом случае, линейная распределенная система будет качественно экспоненциально устойчива с параметрами β и r, если модифицированный пространственный годограф не охватывает линию (Re=-1, Im=0,G) (см. рис.2.4, б).
2.3. Синтез распределенных систем управления Рассмотрим синтез распределенного регулятора для системы управления температурным полем многослойной пластинки (см. рис.2.5.).
Управляющим воздействием служит тепловой поток распределенный по поверхности S1, а функцией выхода – температурное поле T3(x,y,Z *,τ). Поверхности S2, S4, S6 теплоизолированы, а поверхности S3, S5 поддерживаются при постоянной температуре, равной нулю. Для оценки динамических характеристик сформируем математическую модель объекта управления.
Z0=0, Z3=Lz .
Граничные условия для поверхностей S3 и S5
Граничные условия для поверхностей S2 и S4 записываются в виде:
Условия на границах раздела сред, отражающие равенство температур и тепловых потоков, записываются соотношениями:
Управляющее воздействие в виде теплового потока распределено по границе S1
Поверхность S6 теплоизолирована
где: Ставится задача синтеза распределенного регулятора, при котором линейная распределенная система будет качественно экспоненциально устойчива с параметрами β и r. Рассмотрим особенности определения динамических характеристик для распределенных объектов управления и методику синтеза, на примере синтеза регуляторов для системы управления температурным полем многослойной пластинки (см. рис.2.5), математическая модель которой описывается уравнениями (2.3)-(2.9), а геометрические параметры объекта приведены в табл.2.1. Табл.2.1. Геометрические параметры пластины
(Геометрические параметры заданы в системе СИ) Теплофизические параметры заданы следующими значениями
(параметры заданы в системе СИ). Рассматриваемый объект принадлежит к классу пространственно – инвариантных [1,2]. В качестве собственных вектор функций (пространственных мод) выберем функции вида
Вид собственных вектор функций оператора объекта обусловлен граничными условиями (2.4)-(2.5). Определим реакцию объекта на выбранные моды входного воздействия
В рассматриваемом случае поставленная задача решалась численно. Для этого, используя математическую модель объекта, была составлена численная модель и определена реакция объекта на выбранные пространственные моды входного воздействия. Схема дискретизации объекта управления приведена на рис. 2.6. При моделировании объекта управления были выбраны следующие значения переменных: Nx=8; Ny=8; Nz =30; Δx=Lx/(Nx-1); Δy=Ly/(Ny-1); Δz=Lz/(Nz-1). Как известно[1,4], в методике синтеза распределенных регуляторов используют динамические характеристики двух пространственных мод.
Рис. 2.6. Схема дискретизации Методика исследования пространственно - инвариантных объектов и систем приведена в [1-4]. Положим, что в результате моделирования определена реакция объекта (функция выхода) на первую пространственную моду входного воздействия (η=1,γ=1). Эту реакцию представим в виде: График функции
Рис. 2.7. График функции
Аппроксимируем передаточную функцию по выбранным пространственным модам передаточной функцией вида
В результате численного моделирования получены следующие значения параметров передаточной функции: G=(π∙η/Lx)2+ (π∙γ/Ly)2 [1,2]; η=1,γ=1,G1= 66.87, К(G1)= 0.282245, T(G1)= 2058.188584 , τз(G1)= 449.390945 ; η=3,γ=3 , G3= 602.06 , К(G3)= 0.043225, T(G3)= 1120.090859 , τз(G3)= 314.638407 . Используя вычисленные параметры и соотношение (2.10.) были построены годографы функции (2.10.) для выбранных пространственных мод в области s1 =jω1 (см. рис. 2.8,2.9).
Рис.2.8. Модифицированный годограф для G1
Рис.2.9. Модифицированный годограф для G3
Модифицированный пространственный годограф объекта управления приведен на рис. 2.10. Формулировка критерия устойчивости Найквиста для рассматриваемых систем приведена в [12], показано, что для устойчивости замкнутых систем достаточно, что бы модифицированный пространственный годограф не охватывал линию {Re = -1,Im=0, G}. В главе 1 приведены характеристики распределенных звеньев в области s1 =jω1, из которых формируется структура распределенного регулятора. Используем рассмотренные звенья в процедуре синтеза. Передаточная функция пространственно-усилительного звена записывается в виде
Рассматриваемое звено, с использованием обобщенной координаты G [1-5] может быть записано в виде
Рис.2.10. Модифицированный пространственный годограф объекта управления
2.3.1. Методика синтеза распределенного регулятора Рассмотрим синтез распределенного регулятора, реализующего статический закон управления. Передаточная функция такого регулятора имеет вид W= E1∙((n1 -1)/n1+G/n1). Методика синтеза распадается на следующие этапы: 1. Для выбранных пространственных мод (G1 и G3, см. рис. 2.8 ,2.9) определим желаемые коэффициенты усиления регулятора
2. Для определения параметров распределенного регулятора запишем следующие уравнения[1,2 ]
Поделив (2.11) на (2.10), придем к следующему результату:
где Подставляя исходные данные в (2.12), получим
Учитывая ограничение (1≤ n1) [1], выбираем Подставляя вычисленное значение
Синтезированный регулятор может быть записан в виде
(дискретные модели таких регуляторов приведены в [1,2]).
Рис. 2.11. Результаты моделирования замкнутой системы управления
На рис. 2.11. приведен график переходного процесса замкнутой системы управления, построенный по результатам моделирования для дискретной точки объекта (х3=2∙Δх, у3=2∙Δу, z=Z*) (см рис. 2.6.). Аналогичные графики могут быть построены и для других точек.
2.3.2. Методика синтеза пропорционально-интегрального закона управления Рассматриваемая методика использует методы синтеза регуляторов для сосредоточенных систем и методы синтеза распределенных систем управления. 1. В процессе синтеза пропорционально-интегрального закона управления по первой пространственной моде (η=1,γ=1,G1= 66.87, К(G1)= 0.282245,T(G1)= 2058.188584, τз(G1)= 449.390945), частотным методом сосредоточенных систем получен регулятор (при этом параметры были выбраны Δφ=π/6, Δ=1 [1]), передаточная функция которого имеет вид
Модифицированный годограф рассматриваемого регулятора приведен на рис. 2.12.
Рис.2.12. Модифицированный годограф регулятора
2. Синтезированный регулятор состоит из двух блоков - распределенного пространственно-усилительного звена и Wпи
Определение параметров пространственно-усилительного звена распадается на следующие этапы: 2.1. Для выбранных пространственных мод (G1 и G3, см. рис. 2.8,2.9) определим желаемые коэффициенты усиления регулятора
2.2. Для определения параметров распределенного регулятора воспользуемся соотношениями (2.14),(2.13) и (2.12)
Учитывая ограничение (1≤n1), выбираем
Структурная схема синтезированной системы управления приведена на рис.2.13.
Рис.2.13. Структурная схема системы управления
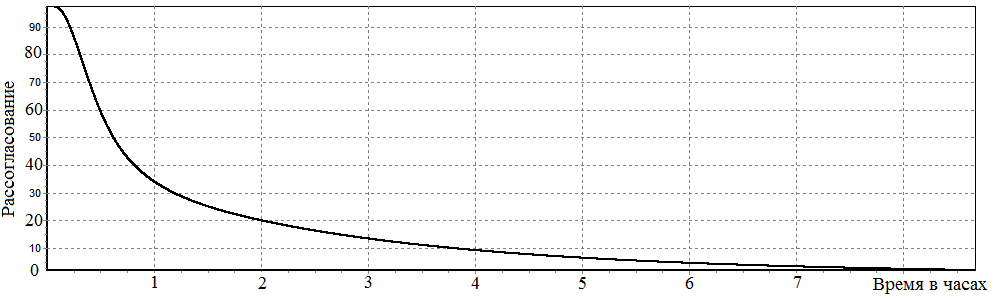
По результатам моделирования замкнутой системы управления построен график функции рассогласования
для заданной точки z=Z*, x=0.2 , y=0.3 (см. рис. 2.14.). Аналогичные графики могут быть построены и для других точек.
Рис. 2.14. График функции рассогласования
2.3.3. Синтеза пропорционально - интегрально-дифференциального закона управления Для синтеза пропорционально - интегрально-дифференциального закона управления разработано множество пакетов программ. Воспользуемся программным комплексом МИРЭА и позволяющим синтезировать различные законы управления и осуществлять анализ работы замкнутых систем управления. В процессе синтеза пропорционально –интегрального -дифференциального закона управления по первой пространственной моде (η=1,γ=1,G1= 66.87, К(G1)= 0.282245, T(G1)= 2058.188584 , τз(G1)= 449.390945), частотным методом сосредоточенных систем получен регулятор, передаточная функция которого имеет вид
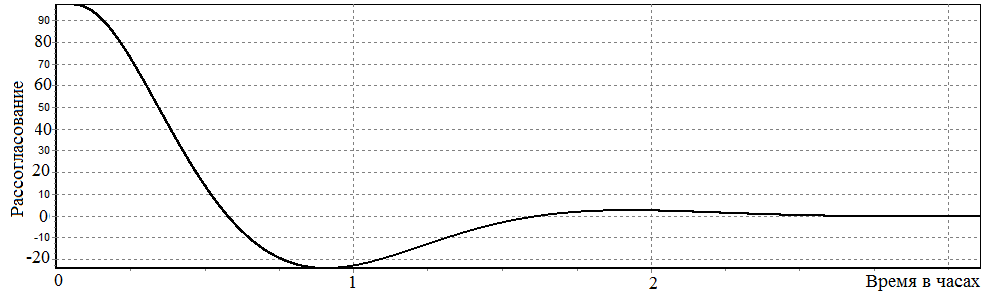
где: К=3.17;Ti=482.4;Td=140.735, π/6≤ Δφ, 10.≤ΔL По результатам моделирования замкнутой системы управления построен график функции рассогласования
для заданной точки z=Z*, x=0.2 , y=0.3 (см. рис. 2.15.). Аналогичные графики могут быть построены и для других точек.
Рис.2.15. График функции рассогласования
2.3.4. Оптимизация процесса выбора значений параметров β и r Проведенные исследования для систем управления объектами, передаточные функции которых описываются в виде
показывают, что статический коэффициент усиления разомкнутой системы определяет устойчивость, точность и динамические характеристики замкнутой системы. Статический коэффициент усиления разомкнутой системы определяется передаточной функцией, приведенной выше и статическим коэффициентом регулятора. Передаточная функция объекта может быть записана в виде
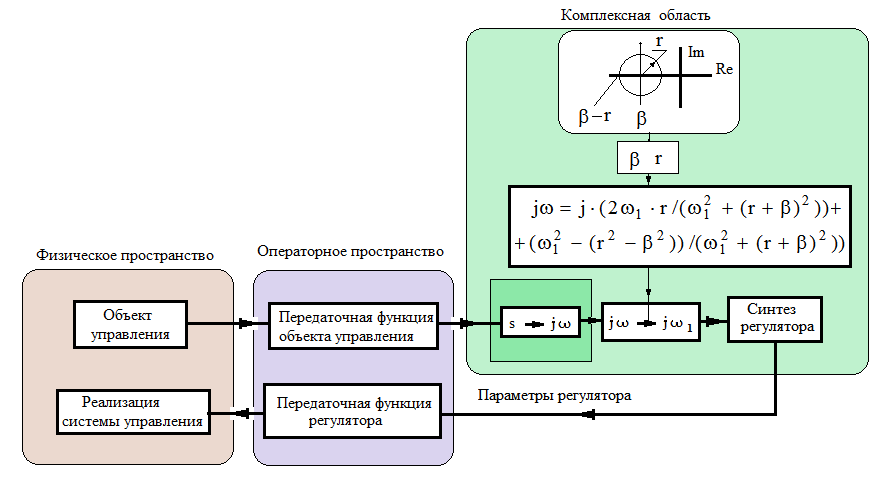
Пространства состояния, используемые при проектировании систем управления, приведены на рис.2.16.
Рис.2.16. Пространства состояния, используемые при проектировании систем управления
Для определения параметров регулятора используется комплексная область jω1. В рассматриваемой области статический коэффициент объекта управления (статическая кривая, см. рис. 2.10) зависит от параметров β и r(см. рис.2.17).
Рис. 2.17. Статическая кривая
Рис.2.18. Поверхность зависимости статики модифицированного годографа от параметров β и r
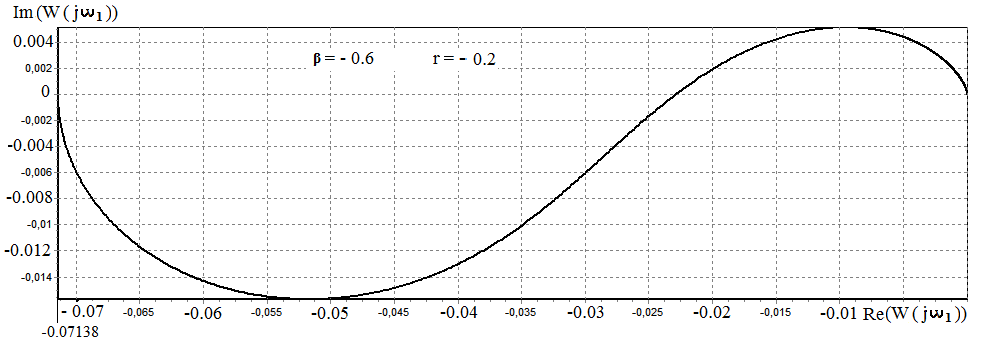
Выберем параметры β и r, обеспечивающие минимальный статический коэффициент усиления объекта управления. Результаты вычислений показывают, что минимальный статический коэффициент зависит от параметров объекта управления. Для объекта (2.10), с параметрами К(G1)= 0.282245, T(G1)= 2058.188584 , τз(G1)= 449.390945, график соотношения r/ β , обеспечивающего минимальный статический коэффициент, приведен на рис.2.18 . Исследуя зависимость статики модифицированного годографа от параметров β и r(результаты исследования приведены на рис. 2.18) получено, что минимальный статический коэффициент усиления модифицированного годографа по первой пространственной моде будет при β=-0.6 и r= - 0.439. Построим модифицированные годографы при вычисленных значениях β и rдля выбранных пространственных мод объекта управления
η=1,γ=1,G1= 66.87, К(G1)= 0.282245, T(G1)= 2058.188584 , τз(G1)= 449.390945 .
Рис.2.19. Модифицированный годограф объекта управления
G3= 602.06 , К(G3)= 0.043225, T(G3)= 1120.090859 , τз(G3)= 314.638407 .
Рис.2.20. Модифицированный годограф объекта управления
Построим модифицированные годографы при вычисленных значениях β и rдля регулятора ПИД: К=3.17; Ti=482.4 ;Td=140.735 (см. рис. 2.21).
Рис.2.21. Модифицированный годограф регулятора
Аналогичные исследования были проведены для разомкнутой системы, состоящей из объекта и регулятора (см. рис.2.22 ).
Рис.2.22. Определение параметров β и rдля разомкнутой системы
Рис.2.23. Модифицированный годограф разомкнутой системы
Построим модифицированный годограф разомкнутой системы управления, состоящей из передаточной функции регулятора ПИД и объекта, по выбранным пространственным модам. При этом выберем значения параметров β= - 0.6 , r= -0.7804878∙ β=0.46829 (см. рис.2.22). Для объекта и регулятора, синтезированного в п.2.3.3 рассмотрим синтез распределенного регулятора, передаточная функция которого имеет вид W= E1(1+ G/n1). Процедура синтеза распадается на следующие этапы: 1. Для выбранных пространственных мод (G1 и G3, см. рис. 2.23) определим желаемые коэффициенты усиления регулятора
2. Для определения параметров распределенного регулятора воспользуемся следующими соотношениями
где Подставляя вычисленное значение
Передаточная функция синтезированного регулятора записывается в виде
где: E1=1.67; n1=148; К=3.17; Ti=482.4 ;Td=140.735.
По результатам моделирования замкнутой системы управления построен график функции рассогласования
для заданной точки z=Z*, x=0.2 , y=0.3 (см. рис. 2.24). Аналогичные графики могут быть построены и для других точек. Как показывают результаты моделирования замкнутой системы (см. рис. 2.24), регулятор достаточно эффективно управляет процессом. Существенное перерегулирование в переходном процессе связано с тем, что реальная передаточная функция объекта по выбранным пространственным модам, описываемая отношением бесконечных полиномов [1,2] , аппроксимирована апериодическим звеном и звеном с чистым запаздыванием (см. 2.10). Это приводит к тому, что динамика реального объекта (в рассматриваемом случае дискретной модели объекта) несколько отличается от динамики объекта (2.10).
Рис.2.24. График переходного процесса
Исследуем влияние лапласиана на переходные процессы . Удалим лапласиан из передаточной функции разомкнутой системы, представляя ее в виде
Графики переходного процесса замкнутой системы приведены на рис. 2. 25
Рис.2.25. График переходного процесса
Графики (см. рис. 2.25, и рис. 2.24) построены по результатам моделирования работы замкнутой системы управления показывают, что, в рассматриваемой системе, влияние лапласиана достаточно существенное. |
||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 297. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,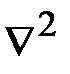 - лапласиан; s -оператор Лапласа;
- лапласиан; s -оператор Лапласа;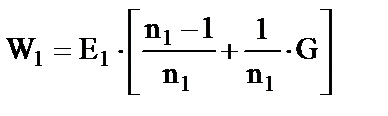 ,
, 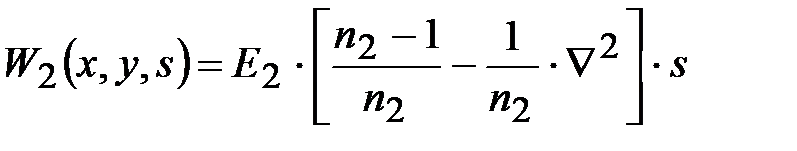 ,
, ,
,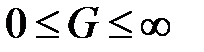 .
. .
.
 ,
, ,
, .
.
 ,
, ,
,  .
. .
.
 ,
, ,
, 


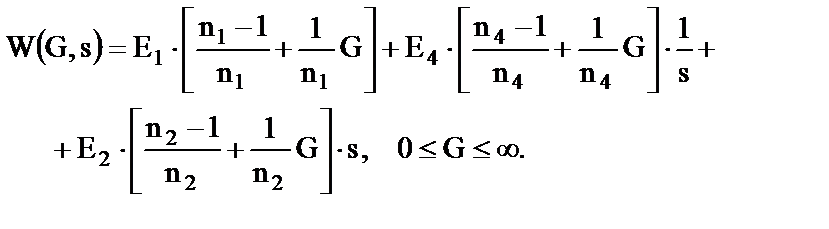


 (2.1)
(2.1) (2.2)
(2.2)



 , (2.3)
, (2.3) ,
,
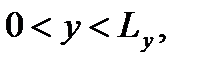


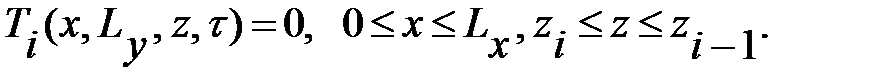 (2.4)
(2.4)
 (2.5)
(2.5)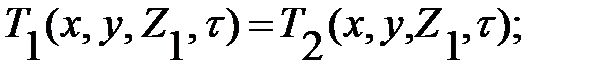
 (2.6.)
(2.6.)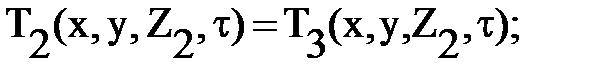
 (2.7)
(2.7) . (2.8)
. (2.8) (2.9)
(2.9) - температурное поле i-ой среды; U(x,y,τ)- управляющее воздействие; x,y,z- пространственные координаты, τ – время.
- температурное поле i-ой среды; U(x,y,τ)- управляющее воздействие; x,y,z- пространственные координаты, τ – время.




 .
. приведен на рис. 2.7.
приведен на рис. 2.7.

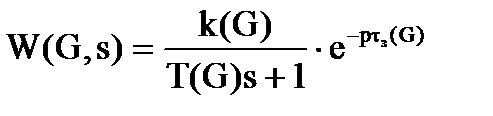 , (2.10)
, (2.10)
 ,(1≤n1<∞).
,(1≤n1<∞).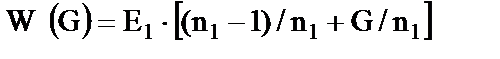 ,(1≤n1<∞).
,(1≤n1<∞).

 ,
, 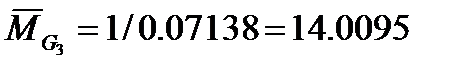 .
. , (2.10)
, (2.10)  . (2.11)
. (2.11) , (2.12)
, (2.12) .
. ,
, 

 в (2.11) и преобразуя, получим
в (2.11) и преобразуя, получим .
.

 , где К=3.889 ,T=1168.70456.
, где К=3.889 ,T=1168.70456.


 , (2.13)
, (2.13)  .(2.14)
.(2.14) ,
,  .
. . (2.15)
. (2.15)
 ,
,
 ,
,
 ,
, .
.








 ,
,  .
. ,
,  .
. .
. ,
,

