
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
ГИДРОЛИТОСФЕРНЫМИ ПРОЦЕССАМИСтр 1 из 9Следующая ⇒ Часть 3. ПРОЕКТИРОВАНИЕ СИСТЕМ УПРАВЛЕНИЯ ВВЕДЕНИЕ Процессы, в окружающей нас среде, неразрывно связаны с пространственными координатами, а их модели описываются уравнениями в частных производных. Системный анализ таких (распределенных) процессов связан усложнением математического аппарата, который опирается на методы решений уравнений в частных производных. Как правило, если найдены решения (реакция объекта на заданное входное воздействие) то эти решения математически могут быть представлены бесконечной совокупностью ортогональных пространственных мод. Обзор методов анализа таких систем управления, а так же используемые подходы при синтезе распределенных систем управления приведен в [1-3]. На сегодняшний день сформировались два направления исследования распределенных процессов (систем): - первое направление основывается на том, что существует аналитическое решение математической задачи, описываемой уравнениями в частных производных. Решение такой задачи строится на основе собственных вектор - функций оператора объекта (некоторого ортогонального базиса). К этому направлению относятся следующие методы: - аналитическое конструирование оптимальных регуляторов для систем с распределенными параметрами (АКОР для СРП), которое основывается на принципе оптимальности Беллмана и принципе максимума Понтрягина. Общим вопросам АКОР для систем с распределенными параметрами посвящены работы Сиразетдинова Т.К. , Дегтярева Г.Л., Егорова А.И. , а также работы Eljai A., Khargonckar P.P. and Poolla K. и др.; - структурный метод анализа систем с распределенными параметрами, основанный на том, существует и может быть найдено фундаментальное решение поставленной краевой задачи. Этот метод рассмотрен в работах Бутковского А.Г. и его школы, а так же развивается в работах  Э. Я. Рапопорта и его учеников, Пустыльникова Л.М., Кубышкин В.А., Финягина В.И., Чубаров Е.П., Martin J. — C. E. ; - частотный метод, который может быть использован для синтеза распределенных регуляторов, в случае, если существует решение математической модели, которое распадается по собственным вектор – функциям оператора объекта. Этот метод может быть использован и для случая, когда динамические характеристики распределенных объектов (по выбранному числу пространственных мод) определяются с использованием экспериментальных данных. Частотный метод синтеза систем с распределенными параметрами подробно изложен в работах[1,4]. - второе направление основывается на методах аппроксимации математических моделей распределенных объектов. По сути, в этом случае мы переходим от распределенных объектов к многомерным сосредоточенным. Бесконечно мерное фазовое пространство в этом случае заменяется конечномерным. Методы конечномерной аппроксимации рассмотрены в литературе достаточно подробно (например, в работах Валеева К.Г.и Жаутыкова О.А.). Многие практические задачи, с использованием методов аппроксимации, успешно решаются в работах Коваля В.А. и его учеников и внедрены в практических системах управления. Однако в теории методов конечномерной аппроксимации распределенных объектов и систем имеется ряд не решенных вопросов, поэтому пользоваться аппроксимацией систем с распределенными параметрами следует весьма осторожно. Переходя от бесконечно мерного фазового пространства к конечномерному, мы не учитываем многие свойства распределенного объекта и, по сути, рассматриваем другой объект. Известна методика аппроксимации передаточных функций по выбранной (η-ой) пространственной моде передаточной функцией вида где s- оператор Лапласа, Тη ,Кη , τη – параметры, определяемые с использованием результатов экспериментальных исследований распределенных объектов. В [1] приведены передаточные функции распределенных объектов управления, математические модели которых описываются уравнениями параболического типа. Передаточные функция объекта по
где: С использованием обобщенной координаты (G), рассматриваемые передаточные функции могут быть записаны в виде:
При достаточно больших значениях
Методика синтеза распределенных регуляторов, разработанная в [1,2], использует динамические характеристики объекта управления. Если математическая модель объекта не имеет аналитического решения, а имеется численная модель (или имеется возможность исследования динамики на реальных объектах), то аппроксимировать передаточную функцию распределенного объекта можно передаточной функцией вида
где где s- оператор Лапласа, a ,К , Δz – параметры, определяемые с использованием результатов экспериментальных исследований распределенных объектов. Положим, что в результате экспериментальных исследований получено: -статический коэффициент по первой пространственной моде входного воздействия (G1) равен К1; - определен статический коэффициент Кη и модуль передаточной функции объекта по η- ой пространственной моде входного воздействия при частоте ω1* (
Решая полученную систему уравнений, определим искомые параметры. Основные подходы к анализу и синтезу систем с распределенными параметрами изложены в [1-6]. Хорошо известно применение качественной теории к синтезу систем с сосредоточенными параметрами, при этом были решены многие практические задачи. Поставим задачу применения качественной теории для синтеза систем управления с распределенными параметрами. Под качественным распределением мод понимается расположение мод (корней) в круге радиуса r больше нуля, с центром в точке (β, j0), причем значении β+r должно быть меньше нуля, то есть данный круг должен лежать в левой полуплоскости комплексной плоскости корней. Рассмотрим применение качественной теории к синтезу распределенных систем управления, передаточные функции которых по отдельным модам могут быть представлены в виде
где s- оператор Лапласа, Тη, Кη, τη – параметры, определяемые с использованием результатов эксперимента. Для того, чтобы замкнутая система имела бы качественное распределение мод потребуем, чтобы все корни характеристического полинома, определяющие расположение мод лежали в круге радиуса r больше нуля, с центром в точке (β, j0), причем значении β+r должно быть меньше нуля, то есть данный круг должен лежать в левой полуплоскости комплексной плоскости корней, где параметр β, определяет среднюю скорость сходимости процессов к положению равновесия, а параметр r– отклонения траекторий движения от их средних значений. Сведем задачу качественного расположения мод к классической задаче определения устойчивости, для чего введем конформное отображение левой полуплоскости комплексной плоскости в единичный круг с центром в начале координат вида [7-12]
а затем применим еще одно конформное отображение, преобразующего единичный круг с центром в начале координат в круг произвольного радиуса r с центром в точке (β, j0), посредством преобразования
тогда характеристический полином замкнутой системы по данной моде Перейдем к частотным передаточным функциям, заменив оператор при этом Согласно принципу приращения аргумента, если разомкнутый контур имеет
где где
Пологая что s=jω , s1= jω1 получим:
Преобразуя, придем к следующему результату
Характеристический полином по каждой пространственной моде замкнутой системы должен иметь все корни, относительно переменной s1, в левой полуплоскости. Все корни должны иметь отрицательные значения вещественных частей, а корни исходного объекта (системы) при этом должны лежать в круге радиуса r больше нуля, с центром в точке (β, j0), причем значения (β+r) должно быть меньше нуля (контур по каждой пространственной моде качественно экспоненциально устойчив с параметрами β и r). Таким образом, Критерия Найквиста применим и для анализа качественного расположение мод в замкнутой распределенной системе.
ГЛАВА 1. ХАРАКТЕРИСТИКИ СТАНДАРТНЫХ РАСПРЕДЕЛЕННЫХ ЗВЕНЬЕВ В ОБЛАСТИ s1 =jω1 Частотная методика синтеза опирается на критерий устойчивости Найквиста, а для формирования структуры регулятора использует «стандартный» набор звеньев. В [1,4] приведен набор распределенных звеньев, из которых формируется структура регулятора в процессе синтеза. Использование качественной теории предполагает анализ динамических характеристик в области s1 =jω1. Рассмотрим динамические характеристики распределенных звеньев [1,4] в области s1 =jω1 .
|
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 206. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 (
(  ),
),
 моде входного воздействия могут быть представлены в виде:
моде входного воздействия могут быть представлены в виде: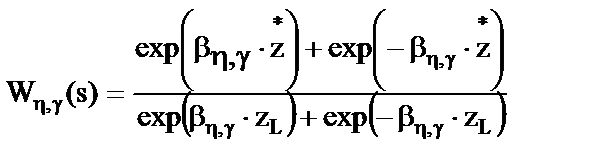 ,
,  ,
, ;
;  - заданные числа;
- заданные числа; ,
,  - пространственные частоты;
- пространственные частоты;  .
. ,
, ,
,  ,
,  .
. , передаточные функции
, передаточные функции  могут быть аппроксимированы передаточной функцией вида
могут быть аппроксимированы передаточной функцией вида , где ΔZ=zL-
, где ΔZ=zL-  .
.
 ,
,  ), который равен
), который равен  . Тогда, для определения параметров, может быть использована следующая система уравнений
. Тогда, для определения параметров, может быть использована следующая система уравнений



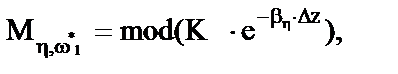
 .
. ,
, , (2)
, (2) должен иметь все корни характеристического полинома относительно переменной
должен иметь все корни характеристического полинома относительно переменной  в круге радиуса rбольше нуля, с центром в точке (β, j0), причем значении β+r должно быть меньше нуля, то есть все корни относительно переменной s1 должны иметь отрицательные вещественные части. При этом вспомогательная передаточная функция (1) с учетом (2) примет вид
в круге радиуса rбольше нуля, с центром в точке (β, j0), причем значении β+r должно быть меньше нуля, то есть все корни относительно переменной s1 должны иметь отрицательные вещественные части. При этом вспомогательная передаточная функция (1) с учетом (2) примет вид . (3)
. (3) в передаточной функции (3) на
в передаточной функции (3) на ,
, . (4)
. (4) корней, лежащих вне круга радиуса r больше нуля, с центром в точке (β, j0), причем значении β+rдолжно быть меньше нуля, а остальные
корней, лежащих вне круга радиуса r больше нуля, с центром в точке (β, j0), причем значении β+rдолжно быть меньше нуля, а остальные  корней располагаются в данном круге, то приращение аргумента вспомогательной частотной передаточной функции (4) должно быть равно
корней располагаются в данном круге, то приращение аргумента вспомогательной частотной передаточной функции (4) должно быть равно
 ,
,  – приращение аргумента вспомогательной частотной передаточной функции. Переходя к амплитудно -фазо-частотной характеристике разомкнутого контура получаем, что приращение аргумента частотной передаточной функции разомкнутого контура (4) относительно точки комплексной плоскости (-1, j0) должно быть равно
– приращение аргумента вспомогательной частотной передаточной функции. Переходя к амплитудно -фазо-частотной характеристике разомкнутого контура получаем, что приращение аргумента частотной передаточной функции разомкнутого контура (4) относительно точки комплексной плоскости (-1, j0) должно быть равно ,
,  – приращение аргумента разомкнутого контура. Если разомкнутый контур качественно экспоненциально устойчив с параметрами β и r, то
– приращение аргумента разомкнутого контура. Если разомкнутый контур качественно экспоненциально устойчив с параметрами β и r, то  = 0. Если приращение аргумента
= 0. Если приращение аргумента  = 0, то амплитудно-фазо-частотная характеристика модифицированной частотной передаточной функции разомкнутого каждого контура
= 0, то амплитудно-фазо-частотная характеристика модифицированной частотной передаточной функции разомкнутого каждого контура  не должна охватывать точку (-1, j0) комплексной плоскости. Сведем задачу установления факта качественного распределения мод к классической задаче определения устойчивости, для чего введем конформное отображение
не должна охватывать точку (-1, j0) комплексной плоскости. Сведем задачу установления факта качественного распределения мод к классической задаче определения устойчивости, для чего введем конформное отображение , или
, или  .
. ,
, . (5)
. (5)