Модель функционирования банка
Набор методов, применяемых для анализа и моделирования банковской деятельности обширен и разнообразен. На протяжении эволюции математической теории банков использовались методы математической статистики, теории оптимального управления, теории случайных процессов, теории игр, теории исследования операций и т.д. Следует помнить, что банк представляет собой сложный объект, требующий комплексного подхода. Создать интегрированную модель банка одновременно охватывающую управление ликвидностью, формирование портфеля активов, формирование кредитно-депозитивной политики и т.д., будет крайне сложно, поэтому мы будем описывать функционирования банка достаточно агрегировано.
Рассмотрим работу банка на достаточно большом интервале времени [  ]. ].
Пусть банк получает доходы в виде оплаты своих услуг за проведение расчетов гарантийных операций, брокерское обслуживание (или другие независящие от портфеля активов доходы) - 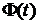 и доходы от приобретенных на свободные средства ценных бумаг составляющих в совокупности портфель банковских активов. и доходы от приобретенных на свободные средства ценных бумаг составляющих в совокупности портфель банковских активов.
Доходы от приобретенных ценных бумаг складываются из процентов по бумагам - 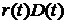 и выплаты вложенных средств при погашении или продаже ценных бумаг - и выплаты вложенных средств при погашении или продаже ценных бумаг - 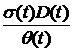 (в случае акции (в случае акции 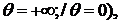
где  - процентная ставка по приобретенным ценным бумагам - процентная ставка по приобретенным ценным бумагам
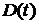 - объем приобретенных ценных бумаг по номиналу - объем приобретенных ценных бумаг по номиналу
 - текущий рыночный курс ценных бумаг приобретенных банком - текущий рыночный курс ценных бумаг приобретенных банком
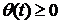 среднее время до погашения ценных бумаг приобретенных банком.[6] среднее время до погашения ценных бумаг приобретенных банком.[6]
В банк поступают, также заемные средства от размещения им своих ценных бумаг со скоростью – W. Мы будем считать, что ценные бумаги эмитированные банком первоначально размещаются а погашаются по номиналу, а процентный доход по ним определяется исходя из ситуации на финансовом рынке в момент эмиссии.
Полученные доходы банк в первую очередьнаправляет на оплату расходов по привлечению средств, которые состоят из выплат процентов по размещенным ценным бумагам - 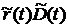 и выплат основных сумм заемных средств - и выплат основных сумм заемных средств - 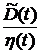 , ,
где  - процентная ставка по размещенным ценным бумагам - процентная ставка по размещенным ценным бумагам
 - объем размещенных ценных бумаг по номиналу - объем размещенных ценных бумаг по номиналу
 - среднее время до погашения ценных бумаг эмитированных банком. - среднее время до погашения ценных бумаг эмитированных банком.
Кроме того, банк несет расходы независящие от объема его пассивов - 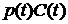 , где: , где:
 - индекс потребительских цен, - индекс потребительских цен,
 - на оплату аренды помещений, на оплату телекоммуникационных расходов, а также других расходов, не зависящих от объема привлеченных средств (пассивов). - на оплату аренды помещений, на оплату телекоммуникационных расходов, а также других расходов, не зависящих от объема привлеченных средств (пассивов).
Затем банк уплачивает необходимые налоги. Оставшиеся средства банк использует для вложения в собственную инфраструктуру (внутренние инвестиции) - 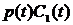 и для дивидендных выплат - и для дивидендных выплат -  . .
Тот факт, что некоторые расходы банк обязан оплачивать из своей чистой прибыли можно учесть путем увеличения сумм расходов путем деления на (1-ставка налогообложения). Существуют также налоги, взимаемые с сумм дохода независимо от понесенных расходов, связанных с получением данного дохода, например налог на пользователей автодорог. Такие налоги можно учесть, заранее умножая сумму дохода на (1-ставка налогообложения). Подобными методами можно учесть и другие особенности, определяемые налоговыми отчислениями, поэтому мы не будем рассматривать ниже проблемы связанные с налогообложением и налоговыми льготами по некоторым ценным бумагам, например государственным. Заметим, что расходы оплачиваются банком в определенном порядке. В первую очередь банк обязан погасить эмитированные ранее ценные бумаги и выплатить проценты по ним, затем он оплачивает расходы, не зависящие от объема пассивов, налоги, и только после этого может выплатить дивиденды.
Если банк располагает свободными денежными средствами, то он направляет ихна покупку ценных бумаг (внешние инвестиции) со скоростью - 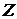 . В случае недостатка средств, ценные бумаги, находящиеся в портфеле банка, могут быть проданы, тогда . В случае недостатка средств, ценные бумаги, находящиеся в портфеле банка, могут быть проданы, тогда 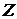 имеет отрицательный знак.[7] имеет отрицательный знак.[7]
Количество денег, ценных бумаг приобретенных банком и ценных бумаг размещенных банком изменяются со временем следующим образом:
 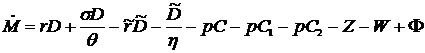 (1.4) (1.4)
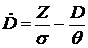 (1.5) (1.5)
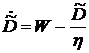 (1.6) (1.6)
Будем считать, что покупка/продажа ценных бумаг принадлежащих банку может быть осуществлена достаточно быстро, но не мгновенно
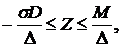 (1.7) (1.7)
где 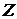 - расход денег на приобретение ценных бумаг (приход денег от их продажи), а - расход денег на приобретение ценных бумаг (приход денег от их продажи), а  - достаточно малая постоянная времени, характеризующая качество активов банка, в смысле ликвидности. Если банк размещает все свои активы на каком-либо одном сегменте финансового рынка, то для него - достаточно малая постоянная времени, характеризующая качество активов банка, в смысле ликвидности. Если банк размещает все свои активы на каком-либо одном сегменте финансового рынка, то для него  есть величина, характеризующая степень развития данного сегмента. В общем случае есть величина, характеризующая степень развития данного сегмента. В общем случае  получается как средневзвешенная по объему активов из величин, характеризующих степень развития каждого из' сегментов финансового рынка, на которых размещены активы. Поскольку мы не рассматриваем проблему формирования активов в данной работе, А предполагается заданной величиной. получается как средневзвешенная по объему активов из величин, характеризующих степень развития каждого из' сегментов финансового рынка, на которых размещены активы. Поскольку мы не рассматриваем проблему формирования активов в данной работе, А предполагается заданной величиной.
Максимальный объем средств, который банк может привлечь путем размещения собственных ценных бумаг ограничен и зависит, в основном, от объема собственного капитала банка, структуры его баланса, качества инвестиционного портфеля банка и от других менее важных показателей его работы. Будем считать, что
 (1.8) (1.8)
где 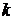 - коэффициент надежности банка, - коэффициент надежности банка, 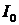 - объем собственных средств банка. - объем собственных средств банка.
Размещение банком собственных ценных бумаг, для привлечения заемных средств, также проходит с некоторой ограниченной скоростью, поэтому
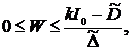 (1.9) (1.9)
где  – постоянная времени, характеризующая степень развитости рынка иных бумаг, эмитируемых банком. Она зависит от того, насколько развита инфраструктура банка, насколько велико число участников рынка, с которыми сотрудничает банк. – постоянная времени, характеризующая степень развитости рынка иных бумаг, эмитируемых банком. Она зависит от того, насколько развита инфраструктура банка, насколько велико число участников рынка, с которыми сотрудничает банк.
Введем переменную  –стоимость портфеля приобретенных ценных бумаг. Тогда уравнения (1.4) – (1.6) примут вид –стоимость портфеля приобретенных ценных бумаг. Тогда уравнения (1.4) – (1.6) примут вид
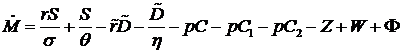
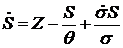
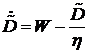
Введем безразмерные управления:  через которые скорость расходования денег на приобретение ценных бумаг и скорость поступления денег от размещения ценных бумаг банка выражаются следующим образом : через которые скорость расходования денег на приобретение ценных бумаг и скорость поступления денег от размещения ценных бумаг банка выражаются следующим образом :
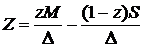
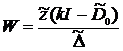
Значение  соответствует скупке/продаже ценных бумаг сторонних эмитентов настолько быстро, насколько это позволяет эффективность рынка ценных бумаг. Значение соответствует скупке/продаже ценных бумаг сторонних эмитентов настолько быстро, насколько это позволяет эффективность рынка ценных бумаг. Значение  соответствует наиболее быстрому привлечению банком заемных средств, а соответствует наиболее быстрому привлечению банком заемных средств, а  - полному отказу от привлечения средств. - полному отказу от привлечения средств.
Основная черта денег – 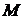 , которая делает их существенно отличными от приобретенных банком ценных бумаг, даже государственных – это возможность их использования для оплаты текущих расходов банка. Поток платежей нельзя осуществить, если нет достаточного запаса денег, следовательно, скорость проведения платежей ограничена и зависит от объема денег: , которая делает их существенно отличными от приобретенных банком ценных бумаг, даже государственных – это возможность их использования для оплаты текущих расходов банка. Поток платежей нельзя осуществить, если нет достаточного запаса денег, следовательно, скорость проведения платежей ограничена и зависит от объема денег:
,  (1.10) (1.10)
где  -характерное время поступления в банк денежных средств (проведения платежей). Ограничения данного вида называют ограничениями ликвидности. -характерное время поступления в банк денежных средств (проведения платежей). Ограничения данного вида называют ограничениями ликвидности.
Платежи, проводимые банком необходимо разбить на две группы:
Обязательные платежи. К ним относятся платежи по погашению ценных бумаг, эмитированных банком -  , выплата процентов по ценным бумагам - , выплата процентов по ценным бумагам -  расходы, не зависящие от объема пассивов - расходы, не зависящие от объема пассивов -  На практике банк может задержать обязательные платежи, но это приведет к серьезным финансовым потерям, а при длительной задержке к признанию его несостоятельным и в итоге к ликвидации. Мы же будем считать, что задержка обязательных платежей полностью исключена, т. е. от банка требуется постоянное сохранение ликвидности. На практике банк может задержать обязательные платежи, но это приведет к серьезным финансовым потерям, а при длительной задержке к признанию его несостоятельным и в итоге к ликвидации. Мы же будем считать, что задержка обязательных платежей полностью исключена, т. е. от банка требуется постоянное сохранение ликвидности.
Необязательные платежи. Проведение данных платежей зависит от руководства и владельцев банка. К ним относятся внутренние инвестиции -  и дивиденды - рС2 . и дивиденды - рС2 .
Для сохранения банком ликвидности необходимо, чтобы:
 для всех для всех 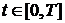 (1.11) (1.11)
Таким образом, мы получаем первое фазовое ограничение для нашей задачи - условие (1.11).
Заметим, что из этого неравенства, при условии неотрицательности  в частности следует, что в частности следует, что 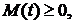 для всех для всех 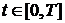
Проведение необязательных платежей, также ограничено по скорости:
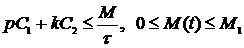
Согласно данному неравенству можно ввести безразмерное управление  так что: так что:
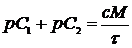 (1.12) (1.12)
Поскольку от объема внутренних инвестиций 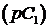 зависит сохранение банком за собой доли на рынке финансовых услуг, можно отнести расходы зависит сохранение банком за собой доли на рынке финансовых услуг, можно отнести расходы 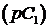 , в каком-то смысле, к обязательным, по крайней мере на большей части участка планирования , в каком-то смысле, к обязательным, по крайней мере на большей части участка планирования 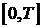 . (После достижения горизонта планирования Т банк может быть ликвидирован его владельцами). Так как дивидендные выплаты не могут быть отрицательными, мы получаем еще одно фазовое ограничение: . (После достижения горизонта планирования Т банк может быть ликвидирован его владельцами). Так как дивидендные выплаты не могут быть отрицательными, мы получаем еще одно фазовое ограничение:
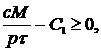 для всех для всех 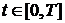 (1.13) (1.13)
Таким образом, мы пришли к тому, что внутренние инвестиции действительно являются обязательными в смысле ограничения (1.13).
Мы будем считать, что на участке планирования банк не получает «сверхдоходов», т. е. больших по сравнению с собственным капиталом прибылей, не зависящих от объема активов. Следовательно, максимальное Количество денег, которое он может привлечь и получит в виде прибыли ограничено некоторой константой  т.е. т.е.  для всех для всех 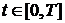 и это третье фазовое ограничение (1.14). и это третье фазовое ограничение (1.14).
Оценку  можно получить исходя из максимального объема заимствований можно получить исходя из максимального объема заимствований  соотношения процентных ставок по привлечению и размещению средств, объема доходов, не зависящих от суммы активов - соотношения процентных ставок по привлечению и размещению средств, объема доходов, не зависящих от суммы активов -  . .
Заметим, что на большей части участка планирования  должно быть близко к нулю, так как банку не выгодно держать наличные деньги не приносящие дохода, ведь на финансовом рынке всегда имеются абсолютно надежные государственные ценные бумаги, приносящие фиксированный положительный доход. должно быть близко к нулю, так как банку не выгодно держать наличные деньги не приносящие дохода, ведь на финансовом рынке всегда имеются абсолютно надежные государственные ценные бумаги, приносящие фиксированный положительный доход.
Отсутствие «сверхдоходов» означает также ограниченность на участке планирования относительной скорости роста курса ценных бумаг:
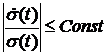
Интересы банка (его владельцев) мы будем описывать стремлением максимизировать дисконтированную полезность будущих дивидендных выплат на достаточно большом интервале времени  Будем считать, что полезность получаемая от немедленной выплаты представляется в Будем считать, что полезность получаемая от немедленной выплаты представляется в 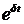 раз больше, чем полезность выплаты того же объема средств, с учетом инфляции, но через время раз больше, чем полезность выплаты того же объема средств, с учетом инфляции, но через время 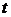 . Коэффициент . Коэффициент 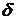 называется коэффициентом дисконтирования полезности дивидендных выплат. Тогда максимизируемый функционал записывается в следующем виде: называется коэффициентом дисконтирования полезности дивидендных выплат. Тогда максимизируемый функционал записывается в следующем виде:
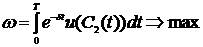 (1.15) (1.15)
где  - функция полезности дивидендных выплат. - функция полезности дивидендных выплат.
Когда  играет роль полезности потребления, обычно требуется, чтобы она была непрерывной, монотонной, вогнутой и ограниченной сверху, а также накладывается на условие играет роль полезности потребления, обычно требуется, чтобы она была непрерывной, монотонной, вогнутой и ограниченной сверху, а также накладывается на условие 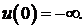 Последнее условие гарантирует положительность текущего потребления в каждый момент времени. Поскольку дивиденды могут не выплачиваться, мы не будем требовать выполнение условия Последнее условие гарантирует положительность текущего потребления в каждый момент времени. Поскольку дивиденды могут не выплачиваться, мы не будем требовать выполнение условия  , полагая, что функция полезности обладает низким отвращением к нулевому потреблению. , полагая, что функция полезности обладает низким отвращением к нулевому потреблению.
Если функция полезности 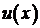 обладает постоянным относительным отвращением к риску по Эрроу-Пратту: обладает постоянным относительным отвращением к риску по Эрроу-Пратту: 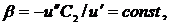 то можно показать, что она может быть записана в виде: то можно показать, что она может быть записана в виде:
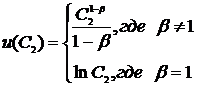
Если считать, что 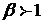 , тогда , тогда  ограничена сверху, но ограничена сверху, но 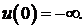
Чтобы избавиться от высокого отвращения к нулевому потреблению  рассмотрим несколько видоизмененную функцию полезности рассмотрим несколько видоизмененную функцию полезности
 (1.16) (1.16)
В этом случае относительное отвращение к риску будет зависеть от объема потребления:  . Исходя из (1.9) и (1.11) получаем . Исходя из (1.9) и (1.11) получаем
 . .
Рассмотрим вместо функции (1.13) прямую, проходящую через точки
 и и 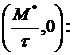
 (1.17) (1.17)
Поскольку 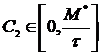 функция (1.17) будет для любого объема дивидендов отрицательна, т. е. ограничена сверху нулем, а также непрерывна и монотонна для любых функция (1.17) будет для любого объема дивидендов отрицательна, т. е. ограничена сверху нулем, а также непрерывна и монотонна для любых  . Такая функция полезности обладает нулевым относительным отвращением к риску по Эрроу-Пратту, а варьируя параметр . Такая функция полезности обладает нулевым относительным отвращением к риску по Эрроу-Пратту, а варьируя параметр  можно менять лишь номинальнуюценность дивидендных выплат. Данный факт подчеркивает отличия в отношении к риску между частным потребителем и коммерческой организацией. С одной стороны, последняя не обладает отвращением к риску, так как может существовать неограниченно долго, по сравнению с продолжительность жизни человека, и не подвержена опасностям, как живые существа. С другой стороны, частный потребитель истративший сумму 2*М рублей получает удовлетворение от первых потраченных М рублей большее, чем от последующих, что определяет вогнутость функции полезности потребления для физических лиц. Мы будем считать, что удвоение дивидендных выплат приводит к удвоению их полезности для получателей, которых достаточно много и в их число входят как физические, так и юридические лица. Это определяет линейность функции полезности дивидендных выплат. В дальнейшем мы будем использовать функцию полезности (1.17). можно менять лишь номинальнуюценность дивидендных выплат. Данный факт подчеркивает отличия в отношении к риску между частным потребителем и коммерческой организацией. С одной стороны, последняя не обладает отвращением к риску, так как может существовать неограниченно долго, по сравнению с продолжительность жизни человека, и не подвержена опасностям, как живые существа. С другой стороны, частный потребитель истративший сумму 2*М рублей получает удовлетворение от первых потраченных М рублей большее, чем от последующих, что определяет вогнутость функции полезности потребления для физических лиц. Мы будем считать, что удвоение дивидендных выплат приводит к удвоению их полезности для получателей, которых достаточно много и в их число входят как физические, так и юридические лица. Это определяет линейность функции полезности дивидендных выплат. В дальнейшем мы будем использовать функцию полезности (1.17).
Таким образом, мы получаем задачу оптимального управления в непрерывном времени
 (1.18) (1.18)
 (1.19) (1.19)
 (1.20) (1.20)
 (1.21) (1.21)
с ограничениями:   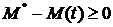 . .
Будем считать, что
 (1.22) (1.22)
 (1.23) (1.23)
Кроме, того, имеется граничное условие  при при 
которое означает, что банк обязан погасить свою задолженность к концу планового периода.
Здесь 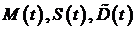 - фазовые переменные, - фазовые переменные, 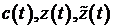 - управления. Здесь - управления. Здесь  - прогнозируемые значения соответствующих переменных - считаются заданными неотрицательными функциями времени, - прогнозируемые значения соответствующих переменных - считаются заданными неотрицательными функциями времени, 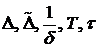 - постоянные, имеющие размерность времени. - постоянные, имеющие размерность времени.
Заметим,если в некоторой точке 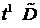 обращается в нуль, то согласно уравнению (1.21) обращается в нуль, то согласно уравнению (1.21)  , т. е. решение в этой точке не убывает. Соответственно, если в некоторой точке , т. е. решение в этой точке не убывает. Соответственно, если в некоторой точке  достигает значения достигает значения 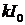 , то , то  т. е. решение не возрастает. Таким образом, при управлениях т. е. решение не возрастает. Таким образом, при управлениях  , из уравнения (1.21), условия , из уравнения (1.21), условия 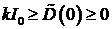 и непрерывности и непрерывности  , мы получаем, что на всем отрезке , мы получаем, что на всем отрезке  объем по номиналу размещенных ценных бумаг банка неотрицателен, т. е. объем по номиналу размещенных ценных бумаг банка неотрицателен, т. е.  , и не превосходит допустимого максимума - , и не превосходит допустимого максимума -  , для всех , для всех  (вообще говоря (вообще говоря 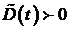 на на  ). ).
Затем, из условия 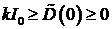 и условий неотрицательности заданных функций, и условий неотрицательности заданных функций, 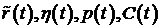 , а также неотрицательности , а также неотрицательности  мы получаем, что мы получаем, что  для всех для всех  . Предполагая непрерывность . Предполагая непрерывность 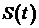 , можно показать, используя уравнение (1.20), что и , можно показать, используя уравнение (1.20), что и 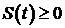 для всех для всех  . Далее мы будем |считать, что . Далее мы будем |считать, что 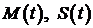 и и  непрерывны, а непрерывны, а 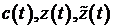 кусочно-непрерывны на кусочно-непрерывны на 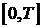 . .
Поскольку  и и 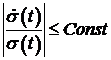 из уравнения (1.20) следует, что из уравнения (1.20) следует, что
 . Используя это неравенство, легко показать существование . Используя это неравенство, легко показать существование  такой, что такой, что  , длявсех , длявсех  . .
Мы не будем, как и предполагалось ранее, рассматривать, как именно формируется портфель приобретаемых банком ценных бумаг в зависимости от надежности, доходности и ликвидности последних, а также от предпочтений руководства банка. Все активы банка будут представлены в агрегированном виде - одной переменной  . .
Из вышеизложенного видно, что кредитно-депозитная политика банка,определяемая в модели управлениями 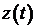 и и  , неразрывно связана сполитикой проведения дивидендных выплат,задаваемой управлением , неразрывно связана сполитикой проведения дивидендных выплат,задаваемой управлением 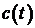 , поэтому далее мы будем исследовать их совместно. , поэтому далее мы будем исследовать их совместно.
Для удобства дальнейшего изучения работы выпишем отдельно обозначения:
 - объем свободных денежных средств банка - наличных денежных знаков в кассе банка, либо денег находящихся на корр. счетах банка в расчетных центрах ЦБ РФ, а также на корр. счетах в других банках - объем свободных денежных средств банка - наличных денежных знаков в кассе банка, либо денег находящихся на корр. счетах банка в расчетных центрах ЦБ РФ, а также на корр. счетах в других банках
 - объем приобретенных ценных бумаг по номиналу - объем приобретенных ценных бумаг по номиналу
 - объем размещенных ценных бумаг по номиналу - объем размещенных ценных бумаг по номиналу
 - доход независящий от объема активов (комиссионные за расчетно-кассовое обслуживание, проведение гарантийных операций, брокерское обслуживание и т. п.) - доход независящий от объема активов (комиссионные за расчетно-кассовое обслуживание, проведение гарантийных операций, брокерское обслуживание и т. п.)
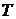 - горизонт планирования - горизонт планирования
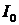 - объем собственных средств банка (капитал) - объем собственных средств банка (капитал)
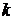 - коэффициент надежности банка - коэффициент надежности банка
 - скорость расходования банком средств на содержание аппарата управления, оплату аренды помещения, и т.д. или расходы независящие от объема пассивов банка в ценах на начальный момент времени - скорость расходования банком средств на содержание аппарата управления, оплату аренды помещения, и т.д. или расходы независящие от объема пассивов банка в ценах на начальный момент времени
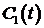 - скорость проведения реинвестиций в инфраструктуру банка (внутренних инвестиций) в ценах на начальный момент времени - скорость проведения реинвестиций в инфраструктуру банка (внутренних инвестиций) в ценах на начальный момент времени
 - скорость проведения дивидендных выплат в ценах на начальный момент времени - скорость проведения дивидендных выплат в ценах на начальный момент времени
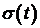 - текущий рыночный курс ценных бумаг приобретенных банком - текущий рыночный курс ценных бумаг приобретенных банком
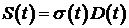 - рыночная стоимость портфеля ценных бумаг банка - рыночная стоимость портфеля ценных бумаг банка
 - постоянная времени, характеризующая степень развития финансового рынка, с учетом распределения активов банка по его секторам - постоянная времени, характеризующая степень развития финансового рынка, с учетом распределения активов банка по его секторам
 - постоянная времени, характеризующая степень развитости рынка ценных бумаг, эмитированных банком - постоянная времени, характеризующая степень развитости рынка ценных бумаг, эмитированных банком
 - номинальный индекс роста портфеля ценных бумаг, приобретенных банком. По каждой приобретенной ценной бумаге номинальная ставка приводится к годовой с учетом реинвестирования, затем вычисляется средневзвешенная по всем ценным бумагам в портфеле банка годовая ставка. Индекс определяется, как ln (1 + «средневзвешенная годовая ставка») - номинальный индекс роста портфеля ценных бумаг, приобретенных банком. По каждой приобретенной ценной бумаге номинальная ставка приводится к годовой с учетом реинвестирования, затем вычисляется средневзвешенная по всем ценным бумагам в портфеле банка годовая ставка. Индекс определяется, как ln (1 + «средневзвешенная годовая ставка»)
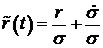 - эффективный индекс роста портфеля ценных бумаг приобретенных банком - эффективный индекс роста портфеля ценных бумаг приобретенных банком
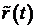 - индекс роста совокупной задолженности по размещенным ценным бумагам. По каждой размещенной ценной бумаге номинальная ставка приводится к годовой, с учетом рефинансирования долга за счет новых размещений бумаг, затем вычисляется средневзвешенная по всем размещенным ценным бумагам годовая ставка. Индекс определяется как ln (1 + + «средневзвешенная годовая ставка») - индекс роста совокупной задолженности по размещенным ценным бумагам. По каждой размещенной ценной бумаге номинальная ставка приводится к годовой, с учетом рефинансирования долга за счет новых размещений бумаг, затем вычисляется средневзвешенная по всем размещенным ценным бумагам годовая ставка. Индекс определяется как ln (1 + + «средневзвешенная годовая ставка»)
 - среднее время погашения ценных бумаг приобретенных банком - среднее время погашения ценных бумаг приобретенных банком 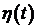 - среднее время погашения ценных бумаг эмитированных банком - среднее время погашения ценных бумаг эмитированных банком  - индекс потребительских цен - индекс потребительских цен
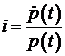 - индекс инфляции - индекс инфляции
 - характерное время проведения платежей (поступления денежных средств) - характерное время проведения платежей (поступления денежных средств)
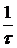 - скорость обращения денег в банковской системе - скорость обращения денег в банковской системе
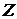 - скорость расходования денег на приобретение ценных бумаг сторонних эмитентов, либо поступления денег от их продажи - скорость расходования денег на приобретение ценных бумаг сторонних эмитентов, либо поступления денег от их продажи
 - скорость поступления денег от размещения ценных бумаг банка - скорость поступления денег от размещения ценных бумаг банка
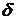 - коэффициент дисконтирования полезности дивидендных выплат - коэффициент дисконтирования полезности дивидендных выплат
 - относительное отвращение к риску по Эрроу-Пратту, параметр используемый при задании функции полезности дивидендных выплат - относительное отвращение к риску по Эрроу-Пратту, параметр используемый при задании функции полезности дивидендных выплат
М* - максимальная суммаденег, которая может принадлежать банку
 - функция полезности дивидендных выплат, непрерывная, монотонная - функция полезности дивидендных выплат, непрерывная, монотонная
 -управление дивидендными выплатами банка -управление дивидендными выплатами банка
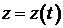 - управление размещением свободных денежных средств банка - управление размещением свободных денежных средств банка
 -управление привлечением в банк денежных средств. -управление привлечением в банк денежных средств.
|


 ].
].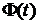 и доходы от приобретенных на свободные средства ценных бумаг составляющих в совокупности портфель банковских активов.
и доходы от приобретенных на свободные средства ценных бумаг составляющих в совокупности портфель банковских активов.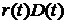 и выплаты вложенных средств при погашении или продаже ценных бумаг -
и выплаты вложенных средств при погашении или продаже ценных бумаг - 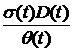 (в случае акции
(в случае акции 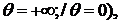
 - процентная ставка по приобретенным ценным бумагам
- процентная ставка по приобретенным ценным бумагам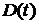 - объем приобретенных ценных бумаг по номиналу
- объем приобретенных ценных бумаг по номиналу - текущий рыночный курс ценных бумаг приобретенных банком
- текущий рыночный курс ценных бумаг приобретенных банком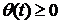 среднее время до погашения ценных бумаг приобретенных банком.[6]
среднее время до погашения ценных бумаг приобретенных банком.[6]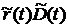 и выплат основных сумм заемных средств -
и выплат основных сумм заемных средств - 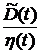 ,
, - процентная ставка по размещенным ценным бумагам
- процентная ставка по размещенным ценным бумагам - объем размещенных ценных бумаг по номиналу
- объем размещенных ценных бумаг по номиналу - среднее время до погашения ценных бумаг эмитированных банком.
- среднее время до погашения ценных бумаг эмитированных банком.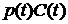 , где:
, где: - индекс потребительских цен,
- индекс потребительских цен, - на оплату аренды помещений, на оплату телекоммуникационных расходов, а также других расходов, не зависящих от объема привлеченных средств (пассивов).
- на оплату аренды помещений, на оплату телекоммуникационных расходов, а также других расходов, не зависящих от объема привлеченных средств (пассивов).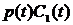 и для дивидендных выплат -
и для дивидендных выплат -  .
.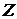 . В случае недостатка средств, ценные бумаги, находящиеся в портфеле банка, могут быть проданы, тогда
. В случае недостатка средств, ценные бумаги, находящиеся в портфеле банка, могут быть проданы, тогда 
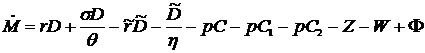 (1.4)
(1.4)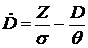 (1.5)
(1.5)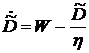 (1.6)
(1.6)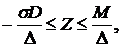 (1.7)
(1.7) - достаточно малая постоянная времени, характеризующая качество активов банка, в смысле ликвидности. Если банк размещает все свои активы на каком-либо одном сегменте финансового рынка, то для него
- достаточно малая постоянная времени, характеризующая качество активов банка, в смысле ликвидности. Если банк размещает все свои активы на каком-либо одном сегменте финансового рынка, то для него  есть величина, характеризующая степень развития данного сегмента. В общем случае
есть величина, характеризующая степень развития данного сегмента. В общем случае  (1.8)
(1.8)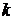 - коэффициент надежности банка,
- коэффициент надежности банка, 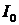 - объем собственных средств банка.
- объем собственных средств банка.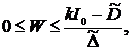 (1.9)
(1.9) – постоянная времени, характеризующая степень развитости рынка иных бумаг, эмитируемых банком. Она зависит от того, насколько развита инфраструктура банка, насколько велико число участников рынка, с которыми сотрудничает банк.
– постоянная времени, характеризующая степень развитости рынка иных бумаг, эмитируемых банком. Она зависит от того, насколько развита инфраструктура банка, насколько велико число участников рынка, с которыми сотрудничает банк. –стоимость портфеля приобретенных ценных бумаг. Тогда уравнения (1.4) – (1.6) примут вид
–стоимость портфеля приобретенных ценных бумаг. Тогда уравнения (1.4) – (1.6) примут вид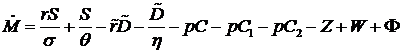
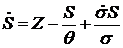
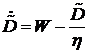
 через которые скорость расходования денег на приобретение ценных бумаг и скорость поступления денег от размещения ценных бумаг банка выражаются следующим образом :
через которые скорость расходования денег на приобретение ценных бумаг и скорость поступления денег от размещения ценных бумаг банка выражаются следующим образом :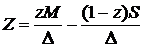
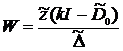
 соответствует скупке/продаже ценных бумаг сторонних эмитентов настолько быстро, насколько это позволяет эффективность рынка ценных бумаг. Значение
соответствует скупке/продаже ценных бумаг сторонних эмитентов настолько быстро, насколько это позволяет эффективность рынка ценных бумаг. Значение  соответствует наиболее быстрому привлечению банком заемных средств, а
соответствует наиболее быстрому привлечению банком заемных средств, а  - полному отказу от привлечения средств.
- полному отказу от привлечения средств.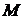 , которая делает их существенно отличными от приобретенных банком ценных бумаг, даже государственных – это возможность их использования для оплаты текущих расходов банка. Поток платежей нельзя осуществить, если нет достаточного запаса денег, следовательно, скорость проведения платежей ограничена и зависит от объема денег:
, которая делает их существенно отличными от приобретенных банком ценных бумаг, даже государственных – это возможность их использования для оплаты текущих расходов банка. Поток платежей нельзя осуществить, если нет достаточного запаса денег, следовательно, скорость проведения платежей ограничена и зависит от объема денег: (1.10)
(1.10) -характерное время поступления в банк денежных средств (проведения платежей). Ограничения данного вида называют ограничениями ликвидности.
-характерное время поступления в банк денежных средств (проведения платежей). Ограничения данного вида называют ограничениями ликвидности. , выплата процентов по ценным бумагам -
, выплата процентов по ценным бумагам -  расходы, не зависящие от объема пассивов -
расходы, не зависящие от объема пассивов -  На практике банк может задержать обязательные платежи, но это приведет к серьезным финансовым потерям, а при длительной задержке к признанию его несостоятельным и в итоге к ликвидации. Мы же будем считать, что задержка обязательных платежей полностью исключена, т. е. от банка требуется постоянное сохранение ликвидности.
На практике банк может задержать обязательные платежи, но это приведет к серьезным финансовым потерям, а при длительной задержке к признанию его несостоятельным и в итоге к ликвидации. Мы же будем считать, что задержка обязательных платежей полностью исключена, т. е. от банка требуется постоянное сохранение ликвидности. и дивиденды - рС2 .
и дивиденды - рС2 . для всех
для всех 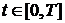 (1.11)
(1.11) в частности следует, что
в частности следует, что 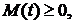 для всех
для всех 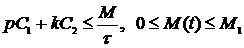
 так что:
так что: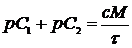 (1.12)
(1.12)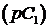 зависит сохранение банком за собой доли на рынке финансовых услуг, можно отнести расходы
зависит сохранение банком за собой доли на рынке финансовых услуг, можно отнести расходы 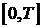 . (После достижения горизонта планирования Т банк может быть ликвидирован его владельцами). Так как дивидендные выплаты не могут быть отрицательными, мы получаем еще одно фазовое ограничение:
. (После достижения горизонта планирования Т банк может быть ликвидирован его владельцами). Так как дивидендные выплаты не могут быть отрицательными, мы получаем еще одно фазовое ограничение: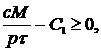 для всех
для всех  т.е.
т.е.  для всех
для всех  соотношения процентных ставок по привлечению и размещению средств, объема доходов, не зависящих от суммы активов -
соотношения процентных ставок по привлечению и размещению средств, объема доходов, не зависящих от суммы активов -  .
. должно быть близко к нулю, так как банку не выгодно держать наличные деньги не приносящие дохода, ведь на финансовом рынке всегда имеются абсолютно надежные государственные ценные бумаги, приносящие фиксированный положительный доход.
должно быть близко к нулю, так как банку не выгодно держать наличные деньги не приносящие дохода, ведь на финансовом рынке всегда имеются абсолютно надежные государственные ценные бумаги, приносящие фиксированный положительный доход.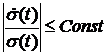
 Будем считать, что полезность получаемая от немедленной выплаты представляется в
Будем считать, что полезность получаемая от немедленной выплаты представляется в 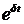 раз больше, чем полезность выплаты того же объема средств, с учетом инфляции, но через время
раз больше, чем полезность выплаты того же объема средств, с учетом инфляции, но через время 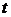 . Коэффициент
. Коэффициент 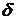 называется коэффициентом дисконтирования полезности дивидендных выплат. Тогда максимизируемый функционал записывается в следующем виде:
называется коэффициентом дисконтирования полезности дивидендных выплат. Тогда максимизируемый функционал записывается в следующем виде: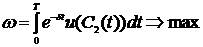 (1.15)
(1.15) - функция полезности дивидендных выплат.
- функция полезности дивидендных выплат.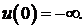 Последнее условие гарантирует положительность текущего потребления в каждый момент времени. Поскольку дивиденды могут не выплачиваться, мы не будем требовать выполнение условия
Последнее условие гарантирует положительность текущего потребления в каждый момент времени. Поскольку дивиденды могут не выплачиваться, мы не будем требовать выполнение условия  , полагая, что функция полезности обладает низким отвращением к нулевому потреблению.
, полагая, что функция полезности обладает низким отвращением к нулевому потреблению.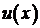 обладает постоянным относительным отвращением к риску по Эрроу-Пратту:
обладает постоянным относительным отвращением к риску по Эрроу-Пратту: 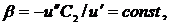 то можно показать, что она может быть записана в виде:
то можно показать, что она может быть записана в виде: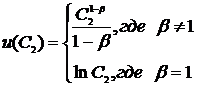
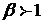 , тогда
, тогда  рассмотрим несколько видоизмененную функцию полезности
рассмотрим несколько видоизмененную функцию полезности (1.16)
(1.16) . Исходя из (1.9) и (1.11) получаем
. Исходя из (1.9) и (1.11) получаем .
. и
и 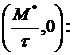
 (1.17)
(1.17)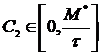 функция (1.17) будет для любого объема дивидендов отрицательна, т. е. ограничена сверху нулем, а также непрерывна и монотонна для любых
функция (1.17) будет для любого объема дивидендов отрицательна, т. е. ограничена сверху нулем, а также непрерывна и монотонна для любых  . Такая функция полезности обладает нулевым относительным отвращением к риску по Эрроу-Пратту, а варьируя параметр
. Такая функция полезности обладает нулевым относительным отвращением к риску по Эрроу-Пратту, а варьируя параметр  можно менять лишь номинальнуюценность дивидендных выплат. Данный факт подчеркивает отличия в отношении к риску между частным потребителем и коммерческой организацией. С одной стороны, последняя не обладает отвращением к риску, так как может существовать неограниченно долго, по сравнению с продолжительность жизни человека, и не подвержена опасностям, как живые существа. С другой стороны, частный потребитель истративший сумму 2*М рублей получает удовлетворение от первых потраченных М рублей большее, чем от последующих, что определяет вогнутость функции полезности потребления для физических лиц. Мы будем считать, что удвоение дивидендных выплат приводит к удвоению их полезности для получателей, которых достаточно много и в их число входят как физические, так и юридические лица. Это определяет линейность функции полезности дивидендных выплат. В дальнейшем мы будем использовать функцию полезности (1.17).
можно менять лишь номинальнуюценность дивидендных выплат. Данный факт подчеркивает отличия в отношении к риску между частным потребителем и коммерческой организацией. С одной стороны, последняя не обладает отвращением к риску, так как может существовать неограниченно долго, по сравнению с продолжительность жизни человека, и не подвержена опасностям, как живые существа. С другой стороны, частный потребитель истративший сумму 2*М рублей получает удовлетворение от первых потраченных М рублей большее, чем от последующих, что определяет вогнутость функции полезности потребления для физических лиц. Мы будем считать, что удвоение дивидендных выплат приводит к удвоению их полезности для получателей, которых достаточно много и в их число входят как физические, так и юридические лица. Это определяет линейность функции полезности дивидендных выплат. В дальнейшем мы будем использовать функцию полезности (1.17). (1.18)
(1.18) (1.19)
(1.19) (1.20)
(1.20) (1.21)
(1.21)

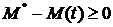 .
. (1.22)
(1.22) (1.23)
(1.23) при
при 
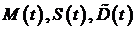 - фазовые переменные,
- фазовые переменные, 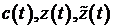 - управления. Здесь
- управления. Здесь  - прогнозируемые значения соответствующих переменных - считаются заданными неотрицательными функциями времени,
- прогнозируемые значения соответствующих переменных - считаются заданными неотрицательными функциями времени, 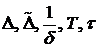 - постоянные, имеющие размерность времени.
- постоянные, имеющие размерность времени.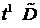 обращается в нуль, то согласно уравнению (1.21)
обращается в нуль, то согласно уравнению (1.21)  , т. е. решение в этой точке не убывает. Соответственно, если в некоторой точке
, т. е. решение в этой точке не убывает. Соответственно, если в некоторой точке  достигает значения
достигает значения 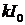 , то
, то  т. е. решение не возрастает. Таким образом, при управлениях
т. е. решение не возрастает. Таким образом, при управлениях  , из уравнения (1.21), условия
, из уравнения (1.21), условия 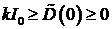 и непрерывности
и непрерывности  , мы получаем, что на всем отрезке
, мы получаем, что на всем отрезке  объем по номиналу размещенных ценных бумаг банка неотрицателен, т. е.
объем по номиналу размещенных ценных бумаг банка неотрицателен, т. е.  , и не превосходит допустимого максимума -
, и не превосходит допустимого максимума -  , для всех
, для всех  (вообще говоря
(вообще говоря 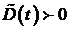 на
на  ).
).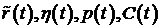 , а также неотрицательности
, а также неотрицательности  для всех
для всех 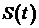 , можно показать, используя уравнение (1.20), что и
, можно показать, используя уравнение (1.20), что и 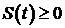 для всех
для всех 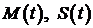 и
и 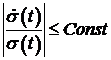 из уравнения (1.20) следует, что
из уравнения (1.20) следует, что . Используя это неравенство, легко показать существование
. Используя это неравенство, легко показать существование  такой, что
такой, что  , длявсех
, длявсех  .
.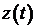 и
и  , неразрывно связана сполитикой проведения дивидендных выплат,задаваемой управлением
, неразрывно связана сполитикой проведения дивидендных выплат,задаваемой управлением 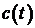 , поэтому далее мы будем исследовать их совместно.
, поэтому далее мы будем исследовать их совместно. - объем приобретенных ценных бумаг по номиналу
- объем приобретенных ценных бумаг по номиналу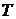 - горизонт планирования
- горизонт планирования - скорость расходования банком средств на содержание аппарата управления, оплату аренды помещения, и т.д. или расходы независящие от объема пассивов банка в ценах на начальный момент времени
- скорость расходования банком средств на содержание аппарата управления, оплату аренды помещения, и т.д. или расходы независящие от объема пассивов банка в ценах на начальный момент времени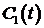 - скорость проведения реинвестиций в инфраструктуру банка (внутренних инвестиций) в ценах на начальный момент времени
- скорость проведения реинвестиций в инфраструктуру банка (внутренних инвестиций) в ценах на начальный момент времени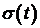 - текущий рыночный курс ценных бумаг приобретенных банком
- текущий рыночный курс ценных бумаг приобретенных банком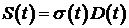 - рыночная стоимость портфеля ценных бумаг банка
- рыночная стоимость портфеля ценных бумаг банка - постоянная времени, характеризующая степень развитости рынка ценных бумаг, эмитированных банком
- постоянная времени, характеризующая степень развитости рынка ценных бумаг, эмитированных банком - номинальный индекс роста портфеля ценных бумаг, приобретенных банком. По каждой приобретенной ценной бумаге номинальная ставка приводится к годовой с учетом реинвестирования, затем вычисляется средневзвешенная по всем ценным бумагам в портфеле банка годовая ставка. Индекс определяется, как ln (1 + «средневзвешенная годовая ставка»)
- номинальный индекс роста портфеля ценных бумаг, приобретенных банком. По каждой приобретенной ценной бумаге номинальная ставка приводится к годовой с учетом реинвестирования, затем вычисляется средневзвешенная по всем ценным бумагам в портфеле банка годовая ставка. Индекс определяется, как ln (1 + «средневзвешенная годовая ставка»)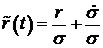 - эффективный индекс роста портфеля ценных бумаг приобретенных банком
- эффективный индекс роста портфеля ценных бумаг приобретенных банком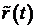 - индекс роста совокупной задолженности по размещенным ценным бумагам. По каждой размещенной ценной бумаге номинальная ставка приводится к годовой, с учетом рефинансирования долга за счет новых размещений бумаг, затем вычисляется средневзвешенная по всем размещенным ценным бумагам годовая ставка. Индекс определяется как ln (1 + + «средневзвешенная годовая ставка»)
- индекс роста совокупной задолженности по размещенным ценным бумагам. По каждой размещенной ценной бумаге номинальная ставка приводится к годовой, с учетом рефинансирования долга за счет новых размещений бумаг, затем вычисляется средневзвешенная по всем размещенным ценным бумагам годовая ставка. Индекс определяется как ln (1 + + «средневзвешенная годовая ставка») - среднее время погашения ценных бумаг приобретенных банком
- среднее время погашения ценных бумаг приобретенных банком 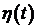 - среднее время погашения ценных бумаг эмитированных банком
- среднее время погашения ценных бумаг эмитированных банком  - индекс потребительских цен
- индекс потребительских цен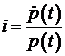 - индекс инфляции
- индекс инфляции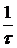 - скорость обращения денег в банковской системе
- скорость обращения денег в банковской системе - скорость поступления денег от размещения ценных бумаг банка
- скорость поступления денег от размещения ценных бумаг банка - функция полезности дивидендных выплат, непрерывная, монотонная
- функция полезности дивидендных выплат, непрерывная, монотонная -управление дивидендными выплатами банка
-управление дивидендными выплатами банка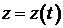 - управление размещением свободных денежных средств банка
- управление размещением свободных денежных средств банка -управление привлечением в банк денежных средств.
-управление привлечением в банк денежных средств.