
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства математического ожидания и дисперсии ⇐ ПредыдущаяСтр 10 из 10 1) 2) 3) 4) Если Случайная величина 5) Если 6) 7) 8) Если 9) 10) 11) Двумерная случайная величина
Здесь
Двумерная случайная величина распределена равномерно в области
Здесь Пример 1.Дискретная двумерная случайная величина
Определить: 1) Законы распределения составляющих 2) условный закон распределения случайной величины 3) 4) коэффициент корреляции Решение.1) Случайная величина Событие, состоящее в том, что случайная величина Аналогично находятся вероятности и других значений случайных величин Законы распределения составляющих будут иметь вид 
2) Условный закон распределения случайной величины
Условный закон распределения случайной величины
Сравнивая закон распределения случайной величины 3) Условное математическое ожидание дискретной случайной величины равно Для решаемой задачи 4) Коэффициент корреляции Корреляционный момент Для решаемой задачи
Вычислим коэффициент корреляции
Пример 2.Пусть задан треугольник АВС с вершинами А(0,0), В(1,0), С(0,1). Обозначим область, ограниченную треугольником АВС через D. Двумерная случайная величина
Найти постоянную
Рис. 3 Решение.1) Постоянную
где
2) Уравнение прямой ВС имеет вид
3) 4) 5)
Пример 3.Пара случайных величин
Известно, что Решение.Совместная нормальность пары случайных величин
Подставляя в последнее соотношение элементы ковариационной матрицы
получим
По условию
Здесь Искомые дисперсии равны, соответственно,
Пример 4.Случайный вектор
Вычислить вектор математических ожиданий Решение.
Ответ:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 331. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
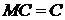 , где
, где 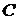 – постоянная.
– постоянная.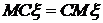 .
.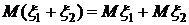 .
.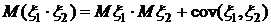 .
.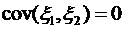 , то
, то 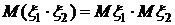 .
.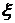 называется неотрицательной
называется неотрицательной 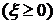 , если она принимает только неотрицательные значения.
, если она принимает только неотрицательные значения.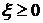 , то
, то  .
.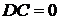 , где
, где 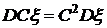 .
.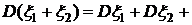
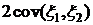 .
.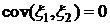 , то
, то 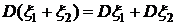 .
.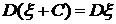 .
. 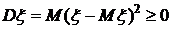 .
.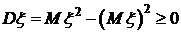
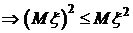 .
.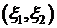 называется распределенной по нормальному закону, если ее плотность распределения
называется распределенной по нормальному закону, если ее плотность распределения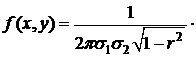
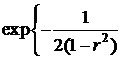
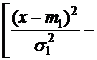
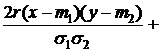
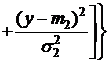 .
.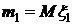 ,
, 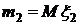 ,
, 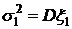 ,
, 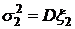 ,
,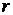 – коэффициент корреляции случайных величин
– коэффициент корреляции случайных величин 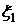 и
и 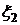 . Для нормальной случайной величины понятия независимости и некоррелируемости эквивалентны.
. Для нормальной случайной величины понятия независимости и некоррелируемости эквивалентны.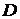 , если ее плотность распределения
, если ее плотность распределения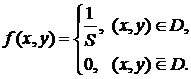
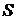 – площадь области
– площадь области 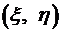 распределена по закону, приведенному в таблице
распределена по закону, приведенному в таблице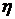
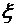 и
и 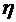 ,
, 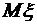 ,
, 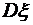 ;
; 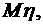
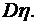
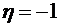 ;
;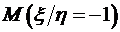 ;
;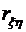 .
.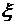 может принимать два значения
может принимать два значения 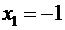 и
и 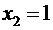 .
. 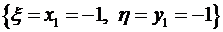 ,
, 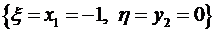 ,
, 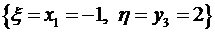 . По теореме сложения вероятностей вероятность события, состоящего в том, случайная величина
. По теореме сложения вероятностей вероятность события, состоящего в том, случайная величина 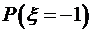 достаточно просуммировать вероятности первой строки двумерного закона распределения.
достаточно просуммировать вероятности первой строки двумерного закона распределения.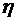 .
.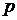
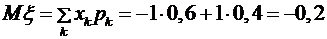 ,
,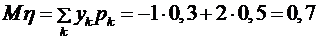 ,
,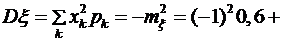
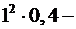
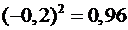 ,
,
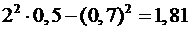 .
.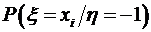 , которые вычисляются по формуле
, которые вычисляются по формуле 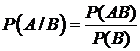 ,
, 
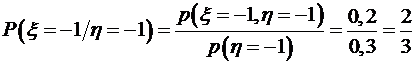 ,
,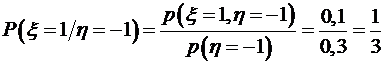 .
.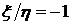
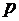
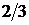
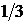
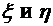 – зависимые случайные величины.
– зависимые случайные величины.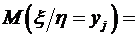
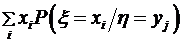 .
.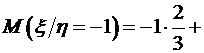
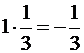 .
.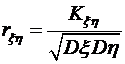 .
.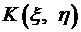 для дискретной двумерной случайной величины равен
для дискретной двумерной случайной величины равен 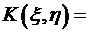
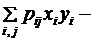
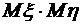 .
.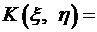
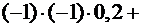
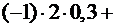
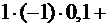
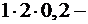

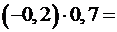
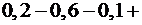
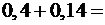
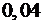 .
.
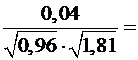
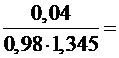
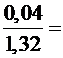
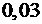 .
.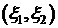 имеет равномерное распределение вероятностей в треугольной области
имеет равномерное распределение вероятностей в треугольной области 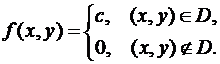
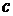 , одномерные плотности
, одномерные плотности 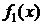 ,
, 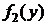 случайных величин
случайных величин 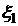 и
и 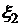 , коэффициент корреляции
, коэффициент корреляции 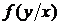 и условное математическое ожидание
и условное математическое ожидание 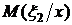 .
.
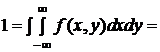
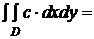
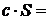
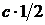 ,
, 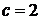 ,
,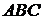 .
. 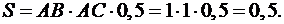 Значит
Значит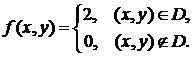
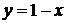 . Тогда область
. Тогда область 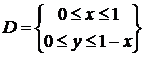 или
или 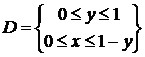 .
.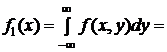
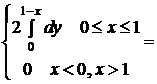
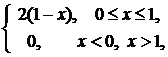
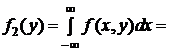
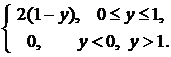
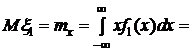
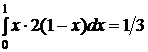 .
.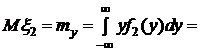
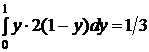 .
.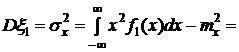
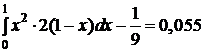 .
.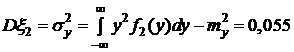 .
.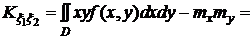
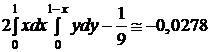 .
.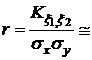
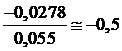 .
.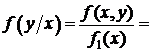
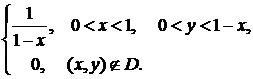
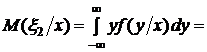
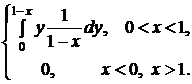
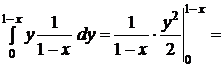
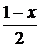 .
.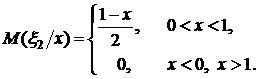
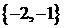 и ковариационной матрицей
и ковариационной матрицей 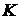 :
: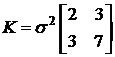 .
.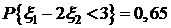 . Найти
. Найти 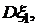
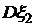 .
.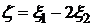 нормальна с параметрами
нормальна с параметрами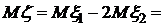
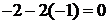 ,
, 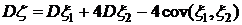 .
.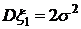 ,
, 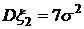 ,
, 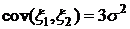 ,
,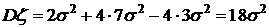 .
.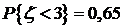 , откуда, используя нормальность
, откуда, используя нормальность 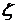 , получаем
, получаем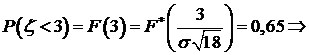
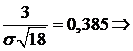
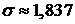 .
.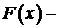 функция распределения вероятности случайной величины
функция распределения вероятности случайной величины  .
.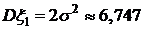 ,
, 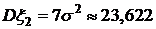 .
.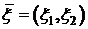 имеет вектор математических ожиданий
имеет вектор математических ожиданий 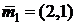 и корреляционную матрицу
и корреляционную матрицу 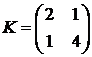 .
.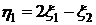 ,
, 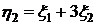 .
.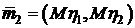 случайного вектора
случайного вектора 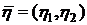 и корреляционную матрицу вектора
и корреляционную матрицу вектора 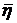 .
.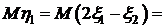
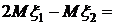
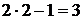 .
.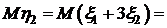
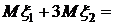
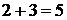 .
.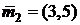 .
. 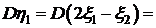
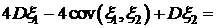
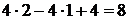 .
.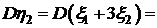
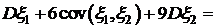
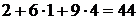 .
.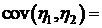
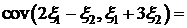
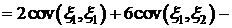
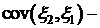
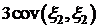 =
=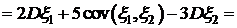
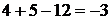 .
.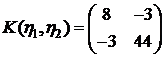 ,
,