
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Классическое определение вероятностиСтр 1 из 10Следующая ⇒ IV. ТЕОРИЯ ВЕРОЯТНОСТИ И МАТЕМАТИЧЕСКАЯ СТАТИСТИКА Справочный материал и принципы решения задач Классическое определение вероятности Под опытом или экспериментом будем понимать всякое осуществление комплекса определенных условий, в результате которых будет происходить интересующее нас явление. Будем считать фиксированным комплекс условий σ, который мы называем опытом, и будем рассматривать некоторую систему событий A, B, C,…, каждое из которых может либо произойти, либо не произойти. Пример 1. Опыт σ: стрельба по мишени. Событие А – попадание по мишени. Событие В – промах. Пример 2.Опыт σ: выбор изделий из партии готовых. Событие А – изделие браковано. Событие В – изделие стандартное. Элементарным событием (или элементарным исходом) называется любой простейший, то есть неделимый в рамках данного эксперимента, исход опыта. Множество всех элементарных исходов будем называть пространством элементарных событий и обозначать Ω. То есть множество исходов опытов образует пространство элементарных событий, если:
Записывают это так: Ω ={w1, w2, …wn,…}={wk , k=1…n, …}. Пример 3. Опыт: подбрасывание монеты 1 раз. Здесь Ω={wг , wц}, где wг – выпадение герба, wц – выпадение цифры. Опыт: монета подбрасывается 2 раза. В данном случае пространство элементарных событий Ω={wг г,wг ц , wц г ,wц ц }. Опыт заключается в определении числа вызовов, поступивших на телефонную станцию за время Т. Здесь Ω={0,1,2.…n,… }.  Любой набор элементарных исходов или произвольное подмножество А Пусть Ω - пространство элементарных событий, S - некоторое подмножество случайных событий, удовлетворяющее следующим условиям:
Иногда требуют большего: для любой бесконечной последовательности событий
Подмножество S, удовлетворяющее этим условиям, называется σ – алгеброй. Пусть задана функция, которая каждому случайному событию из S ставит в соответствие число из интервала [0,1]; Р: S → [0,1], и при этом выполняются следующие аксиомы:
Функцию Р, удовлетворяющую этим аксиомам, называют вероятностью, а значение Р(A) называют вероятностью события А. Определение. Тройка объектов (Ω, S, Р), где Ω – пространство элементарных событий, S – σ-алгебра, Р – вероятность, называется вероятностным пространством. Классическое определение вероятности служит хорошей математической моделью тех случайных явлений, для которых исходов опыта конечное число n и все исходы равновозможны. В классическом определении вероятности полагают:
Иными словами вероятность события Общепринята так же следующая формулировка классического определения вероятности: вероятностью события То есть вероятность события Пример 4. Какова вероятность появления герба, по крайней мере, один раз при двукратном бросании монеты? Решение. Пространство равновозможных элементарных событий данного опыта состоит из следующих событий: Таким образом, Пример 5. Какова вероятность того, что случайно названное двузначное число будет делиться на одиннадцать без остатка? Решение. Так как всех двузначных чисел 90, то число равновозможных исходов данного опыта Пример 6. Какова вероятность того, что в сентябре наугад выбранного года окажется 5 воскресений? Решение. В сентябре любого года 30 дней. Количество воскресений в сентябре зависит от того, какой день недели будет 1-е сентября. 1-е сентября может быть любым днём недели. Так как в неделе 7 дней, то и число всех возможных исходов Пример 7. Имеются пять отрезков длиной 3, 5, 6, 9 и 11 см. Определить вероятность того, что из трех наугад взятых отрезков (из этих пяти) можно построить треугольник. Решение. Имеется Для того чтобы из трех отрезков можно было построить треугольник, необходимо, чтобы больший отрезок был меньше суммы двух других отрезков. Этому условию удовлетворяют следующие исходы
В тех случаях, когда прямой перебор всех возможных исходов становится громоздким, целесообразно использовать комбинаторику.
Элементы комбинаторики Пусть дано множество Первый способ выбора элементов приводит к понятиям перестановок, размещений и сочетаний без повторений или просто перестановок, размещений и сочетаний; второй – к понятиям перестановок, размещений и сочетаний с повторениями. Перестановкой из
Размещением из Число размещений вычисляется по формуле Сочетанием из Число сочетаний
Свойства сочетаний:
Пример 8. Пусть имеется множество Размещения и сочетания с повторениями отличаются от размещений и сочетаний без повторений только тем, что в этих соединениях могут присутствовать повторяющиеся элементы. Число размещений из Число сочетаний из Поскольку в таком виде соединений как перестановки с повторениями участвуют все элементы множества При решении комбинаторных задач могут быть полезны следующие два правила:
Пример 9. Пусть имеется
Если Пример 10. Преподаватель предлагает каждому из трех студентов задумать любое число от 1 до 10. Считая, что выбор каждым студентом любого числа из заданных равновозможен, найти вероятность того, что у кого-то из троих задуманные числа совпадут. Решение. Вначале посчитаем общее количество исходов. Первый из студентов выбирает одно из 10 чисел, Пример 11. По линии связи в случайном порядке передаются все буквы русского алфавита. Найти вероятность того, что на ленте появится последовательность букв, которая начинается словом «мир». Решение. Русский алфавит содержит 33 буквы. Так как по линии связи передаются все буквы, то число равновозможных исходов опыта Следовательно,
Пример 12. Из урны, содержащей 3 шара, три раза наудачу вынимается по одному шару с возвращением каждый раз обратно. Найти вероятность того, что в руке перебывают все шары. Решение. По условию задачи шары возвращаются в урну, следовательно, имеем схему выбора элементов с возвращением. Число всех возможных исходов данного опыта – это число размещений из трех элементов по три с повторениями, то есть
Благоприятными событию A={
Пример 13. Технический контроль проверяет из партии в 500 деталей 20 деталей, взятых наудачу. Партия содержит 15 нестандартных деталей. Какова вероятность того, что среди проверяемых деталей будет ровно две нестандартные? Решение. Так как по условию задачи 20 деталей из 500 извлекаются наудачу, то все возможные варианты извлечения 20 деталей из 500 естественно считать равновозможными и для нахождения требуемой вероятности воспользоваться классической схемой (классическим определением вероятности). Порядок следования стандартных и нестандартных деталей в извлекаемых 20 не играет роли. Важно только количество стандартных и нестандартных деталей. Следовательно, количество всех возможных способов, которыми это можно сделать, равно Событию
Пример 14.Трехзначное число составляется следующим образом: бросаются три игральные кости: белая, синяя и красная; число выпавших очков на белой кости – это число сотен, число выпавших очков на синей кости – это число десятков, а число выпавших очков на красной кости – это число единиц трехзначного числа. Какова вероятность того, что полученное таким образом число будет больше 456? Решение. Количество всех чисел, которые можно получить указанным способом, в соответствие с правилом произведения, будет равно Посчитаем количество исходов опыта, благоприятных появлению события А. Числа, большие 456, будут получаться, если число сотен будет больше 4, то есть 5 или 6 или число сотен будет равно 4, а число десятков будет больше чем 5, то есть 6. Пусть число сотен будет равно 5. Таких опытов будет Пример 15.Трем радиостанциям разрешена работа на шести различных частотах. Определить вероятность того, что, по крайней мере, две радиостанции будут работать на одинаковых частотах, если выбор частот производится наугад. Решение. Число всех равновозможных исходов опыта – это число размещений из шести элементов (частот) по три с повторениями, то есть Таким образом, Следовательно,
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 424. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 в результате опыта один из исходов обязательно происходит;
в результате опыта один из исходов обязательно происходит; Ω называется случайным событием.
Ω называется случайным событием.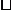 Множество S – замкнуто относительно операций сложения, умножения и отрицания.
Множество S – замкнуто относительно операций сложения, умножения и отрицания. .
. события принадлежат S.
события принадлежат S.
 ,
,  .
.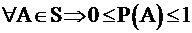 ,
, "i,j, і≠ј,
"i,j, і≠ј, .
. ;
; равной
равной .
. равна отношению числа элементарных событий
равна отношению числа элементарных событий  , входящих в
, входящих в  .
. называется отношение числа
называется отношение числа  исходов опыта, благоприятствующих появлению события
исходов опыта, благоприятствующих появлению события  равновозможных исходов опыта.
равновозможных исходов опыта. определяется как
определяется как  Событие
Событие  . Следовательно,
. Следовательно, 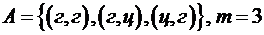 .
. .
. . Из этих чисел на 11 без остатка делятся 11, 22, 33, 44, 55, 66, 77, 88, 99. Следовательно, число исходов, благоприятствующих событию {двузначное число будет делиться на одиннадцать без остатка}
. Из этих чисел на 11 без остатка делятся 11, 22, 33, 44, 55, 66, 77, 88, 99. Следовательно, число исходов, благоприятствующих событию {двузначное число будет делиться на одиннадцать без остатка}  . Искомая вероятность будет равна
. Искомая вероятность будет равна  .
. . Если сентябрь начнется с понедельника, вторника, среды, четверга или пятницы то воскресений будет 4. Если сентябрь начнется с субботы или воскресенья, то воскресений будет 5. Среди 7 равновозможных исходов 2 будут благоприятны событию {в сентябре наугад выбранного года окажется 5 воскресений}, следовательно,
. Если сентябрь начнется с понедельника, вторника, среды, четверга или пятницы то воскресений будет 4. Если сентябрь начнется с субботы или воскресенья, то воскресений будет 5. Среди 7 равновозможных исходов 2 будут благоприятны событию {в сентябре наугад выбранного года окажется 5 воскресений}, следовательно,  . Искомая вероятность
. Искомая вероятность  .
. равновозможных исходов данного опыта:
равновозможных исходов данного опыта:  ,
,  ,
,  ,
, 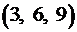 ,
, 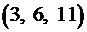 ,
,  ,
,  ,
,  ,
,  ,
,  .
. . Следовательно,
. Следовательно, .
. вычисляется по формуле
вычисляется по формуле .
. .
. вычисляется по формуле
вычисляется по формуле .
.

 из трёх элементов. Тогда все размещения двух элементов из трёх таковы:
из трёх элементов. Тогда все размещения двух элементов из трёх таковы:  Все перестановки множества
Все перестановки множества  имеют вид:
имеют вид:  и
и  Все сочетания двух элементов из множества
Все сочетания двух элементов из множества 
 .
. .
. элементов первого типа,
элементов первого типа,  элементов второго типа, …,
элементов второго типа, …,  элементов
элементов  го типа
го типа  , то число перестановок с повторениями вычисляется по формуле
, то число перестановок с повторениями вычисляется по формуле  .
. может быть выбран
может быть выбран  способами.
способами. способами.
способами.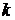 групп элементов, причем
групп элементов, причем  -я группа состоит из
-я группа состоит из  – элементов. Выберем по одному элементу из каждой группы, тогда общее число
– элементов. Выберем по одному элементу из каждой группы, тогда общее число  способов, которыми можно произвести такой выбор по правилу произведения
способов, которыми можно произвести такой выбор по правилу произведения . (1)
. (1) , то можно считать, что выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда
, то можно считать, что выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда  .
. Второй и третий делают то же самое,
Второй и третий делают то же самое,  Согласно формуле (1), общее число способов будет равно
Согласно формуле (1), общее число способов будет равно  Подсчитаем число благоприятных исходов. Для этого сначала найдем общее число комбинаций задуманных чисел, в которых нет совпадений. Первый студент может выбрать любое из 10 чисел, второй любое из 9 чисел, а третий студент – любое из оставшихся 8 чисел. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, по формуле (1) равно
Подсчитаем число благоприятных исходов. Для этого сначала найдем общее число комбинаций задуманных чисел, в которых нет совпадений. Первый студент может выбрать любое из 10 чисел, второй любое из 9 чисел, а третий студент – любое из оставшихся 8 чисел. Поэтому общее число комбинаций задуманных чисел, в которых нет совпадений, по формуле (1) равно  Остальные случаи (1000 – 720 =280) характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность равна
Остальные случаи (1000 – 720 =280) характеризуются наличием хотя бы одного совпадения. Следовательно, искомая вероятность равна 
 . Из этих исходов благоприятными появлению события {появится последовательность букв, которая начинается словом «мир»} будут все исходы, в которых на первых трех позициях будет стоять слово «мир» (такому выбору соответствует один исход), а остальные позиции будут заполнены любым образом (число таких вариантов
. Из этих исходов благоприятными появлению события {появится последовательность букв, которая начинается словом «мир»} будут все исходы, в которых на первых трех позициях будет стоять слово «мир» (такому выбору соответствует один исход), а остальные позиции будут заполнены любым образом (число таких вариантов  ). По правилу произведения число благоприятных исходов
). По правилу произведения число благоприятных исходов  .
. .
. .
. } будут те исходы, в которых элементы (шары) не будут повторяться. Число таких исходов – это число размещений из трех элементов по три, или число перестановок из трех элементов, то есть
} будут те исходы, в которых элементы (шары) не будут повторяться. Число таких исходов – это число размещений из трех элементов по три, или число перестановок из трех элементов, то есть  . Так как все исходы опыта равновозможные, то
. Так как все исходы опыта равновозможные, то .
. , то есть
, то есть  .
. исходов, то есть
исходов, то есть  . Таким образом,
. Таким образом, .
. .
. 
 так как число десятков и единиц может произвольно меняться от 1 до 6. Такие же рассуждения справедливы, если число сотен равно 6. Опытов, у которых первые две цифры 45 будет 6. Используя правила произведения и суммы, найдем количество таких чисел
так как число десятков и единиц может произвольно меняться от 1 до 6. Такие же рассуждения справедливы, если число сотен равно 6. Опытов, у которых первые две цифры 45 будет 6. Используя правила произведения и суммы, найдем количество таких чисел 
 . Так как все исходы опыта равновозможные, то искомая вероятность
. Так как все исходы опыта равновозможные, то искомая вероятность  .
. . Благоприятными событию A={по крайней мере, две радиостанции будут работать на одинаковых частотах} будут те исходы, в которых элементы (частоты) будут повторяться. Число таких исходов –
. Благоприятными событию A={по крайней мере, две радиостанции будут работать на одинаковых частотах} будут те исходы, в которых элементы (частоты) будут повторяться. Число таких исходов –  и три радиостанции работают на одной частоте –
и три радиостанции работают на одной частоте –  . Число исходов, в которых две из трех радиостанций могут работать на одной из шести частот, – это
. Число исходов, в которых две из трех радиостанций могут работать на одной из шести частот, – это  . Число различных частот – 6. Третья радиостанция может работать на одной из пяти «незанятых» частот. По правилу произведения
. Число различных частот – 6. Третья радиостанция может работать на одной из пяти «незанятых» частот. По правилу произведения 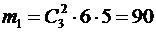 . Очевидно, что число исходов
. Очевидно, что число исходов  .
. .
. .
.