
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Двумерные случайные величиныВектор Если координаты вектора Закон распределения дискретной двумерной случайной величины
где Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения составляющих, то есть случайных величин Если функцию распределения вероятности вектора
Свойства функции и плотности распределения вероятности 1) 2) 3) 4) 5) 6) В любой точке непрерывности функции 7) 8) 9) 10) где Условной плотностью распределения случайной величины  Аналогично определяют Равенство Случайные величины Случайные величины независимы, если выполняется любое из условий:
Для двумерных случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математические ожидания Условным математическим ожиданием для дискретного случайного вектора называется сумма: Для двумерных непрерывных случайных величин условным математическим ожиданием называется интеграл: Величина Если
где Для дискретного случайного вектора
Величина Если
Свойства корреляционного момента и коэффициента корреляции 1) 2) Если 3) Если 4) 5) 6) 7)
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 315. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 , координаты которого есть случайные величины, заданные на одном и том же вероятностном пространстве, называется случайным вектором, а функция
, координаты которого есть случайные величины, заданные на одном и том же вероятностном пространстве, называется случайным вектором, а функция  называется функцией распределения вероятности случайного вектора
называется функцией распределения вероятности случайного вектора  или двумерной случайной величины
или двумерной случайной величины  представляет собой таблицу
представляет собой таблицу











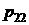


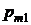


 Так же как и для одномерной дискретной случайной величины должно выполняться условие нормировки
Так же как и для одномерной дискретной случайной величины должно выполняться условие нормировки  .
. и
и  , то случайную величину
, то случайную величину  называют непрерывной двумерной случайной величиной, а
называют непрерывной двумерной случайной величиной, а  – ее плотностью распределения вероятности.
– ее плотностью распределения вероятности.



 .
.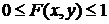 .
.

 0.
0. .
. ,
,  , где
, где  и
и  – функции распределения вероятности случайных величин
– функции распределения вероятности случайных величин 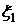 и
и 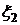 .
.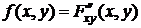 .
. .
. .
. .
. ,
,  ,
,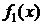 и
и 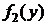 – плотности распределения случайных величин
– плотности распределения случайных величин  при условии, что
при условии, что  называют функцию
называют функцию  ,
, 
 ,
, 
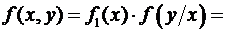
 называют теоремой умножения плотностей вероятности.
называют теоремой умножения плотностей вероятности. ,
,  случайные события
случайные события  и
и  независимы (см. стр.12).
независимы (см. стр.12).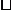

 .
. или
или  .
. ,
,  и дисперсии
и дисперсии  ,
,  составляющих, а также условные математические ожидания и корреляционный момент.
составляющих, а также условные математические ожидания и корреляционный момент.


 называется корреляционным моментом (ковариацией) двух случайных величин
называется корреляционным моментом (ковариацией) двух случайных величин 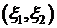 – непрерывная двумерная случайная величина с плотностью распределения
– непрерывная двумерная случайная величина с плотностью распределения 

 ,
,
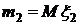 .
.

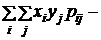
 .
. называется коэффициентом корреляции случайных величин
называется коэффициентом корреляции случайных величин  , то случайные величины
, то случайные величины  .
. . Обратное неверно: из некоррелируемости случайных величин не следует их независимость.
. Обратное неверно: из некоррелируемости случайных величин не следует их независимость. , то
, то 
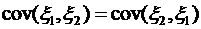 .
.  .
. .
.
 .
.