
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Свойства плотности распределения вероятности непрерывной случайной величины1) 2) 3) 4) Замечание.Для функции распределения
где
Для случайных величин вводят понятия начальных и центральных моментов, из которых наиболее часто используются математическое ожидание и дисперсия. Математическим ожиданием случайной величины
Говорят, что математическое ожидание у случайной величины существует, если ряд (интеграл) (1) сходится абсолютно. Дисперсией случайной величины
Дисперсия вычисляется по формулам:
Рассеивание возможных значений случайной величины от её математического ожидания часто характеризуют средним квадратическим отклонением Существует достаточно большое число законов распределения дискретных и непрерывных величин, которые встречаются в приложениях. Параметры этих законов являются числовыми характеристиками случайных величин или же числовые характеристики выражаются через параметры законов распределения.
Примеры распределений дискретных случайных величин
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 365. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
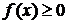 .
. .
.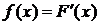 в любой точке непрерывности
в любой точке непрерывности 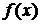 .
.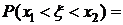

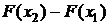 .
.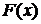 дискретной случайной величины справедлива формула
дискретной случайной величины справедлива формула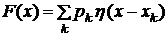 ,
,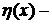 функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле
функция Хэвисайда. Дифференцируя последнее равенство, видим, что и для дискретной случайной величины можно ввести плотность распределения вероятности по формуле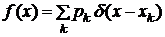 .
.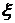 называется число
называется число (1)
(1)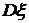 называется число
называется число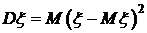 .
.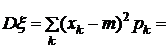
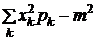 для дискретной случайной величины.
для дискретной случайной величины.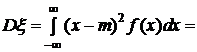
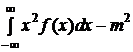 для непрерывной случайной величины, где
для непрерывной случайной величины, где 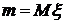 .
.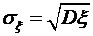 .
.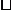 Биномиальное распределение
Биномиальное распределение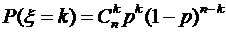
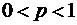 ,
, 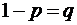 ,
, 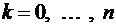 ,
, ,
, 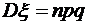 .
.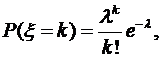
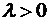 ,
, 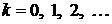 ,
, 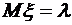 ,
, 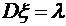 .
.