
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Геометрическое определение вероятностиГеометрическое определение обобщает классическое определение вероятности на случай, когда пространство элементарных событий При этом на прямой будем рассматривать лишь промежутки или их объединения, то есть подмножества, которые имеют длину, на плоскости – те подмножества, которые имеют площадь и т.д. Под мерой В этом случае вероятность считается по формуле:
Пример 1. Телефонная линия длиной 2 км, соединяющая пункты Решение. Точка
Пример 2.В эллипс с полуосями 2 и 3 наудачу ставится точка. Какова вероятность того, что она попадет во вписанную в эллипс окружность, центр которой совпадает с центром эллипса? Решение. Точка  Пример 3. Две точки независимо друг от друга наудачу выбираются на отрезке 1. Определяем пространство элементарных событий. Пусть Итак, пространство элементарных событий совпадает с квадратом D. Выбрать две точки отрезка 2. Равновозможность элементарных исходов гарантирована методикой проведения случайного эксперимента, поскольку, как сказано в условии задачи, обе точки выбираются на отрезке наудачу. Соответственно, ни один из участков квадрата D не является более предпочтительным, чем любой другой равный ему по площади участок квадрата D. 3. Нас интересует вероятность события Ему соответствует область
Рис. 1 Находим площадь Находим площадь
Согласно геометрическому определению вероятности
Ответ. Пример 4.Для поражения точечной воздушной цели достаточно разрыва снаряда на расстоянии 10 м от неё. Из-за ошибок прицеливания разрыв снаряда равновозможен в любой точке эллипсоида с центром в точки цели и полуосями 20, 20 и 60 м. Какова вероятность того, что цель будет поражена? Решение. Точка Событие Следовательно,
|
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 347. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
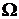 представляет собой подмножество пространства
представляет собой подмножество пространства  .
.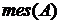 множества
множества  будем понимать его длину, площадь или объем, в зависимости от того, к какому пространству принадлежит
будем понимать его длину, площадь или объем, в зависимости от того, к какому пространству принадлежит  или
или  . Будем считать, что
. Будем считать, что  , и вероятность попадания случайно брошенной точки в любое подмножество
, и вероятность попадания случайно брошенной точки в любое подмножество  .
. и
и 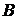 , порвалась в неизвестном месте. Считая обрыв равновозможным в любой точке линии, найти вероятность того, что обрыв находится не далее чем 450 м от пункта
, порвалась в неизвестном месте. Считая обрыв равновозможным в любой точке линии, найти вероятность того, что обрыв находится не далее чем 450 м от пункта 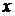 – место обрыва линии может с одинаковой вероятностью занимать любое положение на отрезке длиной 2000 м. Следовательно, множество
– место обрыва линии может с одинаковой вероятностью занимать любое положение на отрезке длиной 2000 м. Следовательно, множество 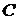 , состоящее в том, что обрыв произошел на расстоянии не более 450 от пункта
, состоящее в том, что обрыв произошел на расстоянии не более 450 от пункта  и
и .
. может с одинаковой вероятностью занимать любое положение в области, ограниченной эллипсом. Следовательно, множество
может с одинаковой вероятностью занимать любое положение в области, ограниченной эллипсом. Следовательно, множество  .
.  . Событие
. Событие 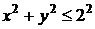 .
.  . Следовательно,
. Следовательно, 
 . Найти вероятность того, что произведение координат точек будет больше 0,4.
. Найти вероятность того, что произведение координат точек будет больше 0,4.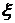 и
и  координаты первой и второй точек, выбранных на
координаты первой и второй точек, выбранных на  вещественных чисел. Каждой такой паре соответствует точка квадрата
вещественных чисел. Каждой такой паре соответствует точка квадрата  на плоскости XOY. Наоборот, каждой точке
на плоскости XOY. Наоборот, каждой точке  , то есть некоторый исход случайного эксперимента.
, то есть некоторый исход случайного эксперимента.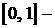 это то же самое, что выбирать одну точку квадрата D.
это то же самое, что выбирать одну точку квадрата D. .
. (см. рис.1).
(см. рис.1).
 области
области 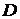 . Очевидно, что
. Очевидно, что  .
. области
области  . Имеем
. Имеем .
. .
. .
. может с одинаковой вероятностью занимать любое положение в области, ограниченной эллипсоидом. Следовательно, множество
может с одинаковой вероятностью занимать любое положение в области, ограниченной эллипсоидом. Следовательно, множество  .
.  .
.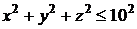 .
.  .
. .
.