
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Эмпирические функции распределения. Полигон и гистограмма.Предположим, что имеется выборка
О. Случайная величина Y называется выборочной или эмпирической. Ряд распределения случайной величины Y называется выборочным или эмпирическим. О.Эмпирической функцией распределения называется функция распределения выборочной (эмпирической) случайной величины Y. Обозначается эта функция: О. Последовательность значений Пусть из генеральной совокупности извлечена выборка, причем О. Наблюдаемые значения Числа наблюдений О. Статистическим распределением выборки называют перечень вариант и соответствующих им частот или относительных частот.
Точечные оценки неизвестных параметров. Несмещенные, состоятельные, эмпирические оценки. Предположим, что имеется выборка О1. Оценкой или статистикой параметра О2. Оценка О3. Оценка  О4. Несмещенная оценка ┐ Пример: Предположим, что имеется выборка В качестве оценки 1.
Методы получения оценок. Метод моментов. Пусть Тогда 1. При любом фиксированном 2. Проверим состоятельность оценки
|
||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 169. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 из генеральной совокупности с функцией распределения F(x). Через Y обозначим случайную величину с рядом распределения (законом распределения)
из генеральной совокупности с функцией распределения F(x). Через Y обозначим случайную величину с рядом распределения (законом распределения)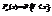 .
. 
 , где
, где 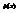 - число выборочных значений
- число выборочных значений 



 , записанных в возрастающем порядке
, записанных в возрастающем порядке  где
где 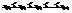 называется вариационным рядом выборки.
называется вариационным рядом выборки. наблюдалось
наблюдалось  раз,
раз,  раз, …,
раз, …,  раз и
раз и  - объем выборки.
- объем выборки. называют вариантами.
называют вариантами. называют частотами, а их отношения к объему выборки
называют частотами, а их отношения к объему выборки  - относительными частотами.
- относительными частотами. (например, функция распределения
(например, функция распределения  ).
). от выборочных значений
от выборочных значений 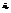 неизвестного параметра
неизвестного параметра  .
.
 )
)  .
.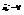
 несмещенная оценка параметра
несмещенная оценка параметра 
 ,
,  . Здесь
. Здесь  - генеральная дисперсия.
- генеральная дисперсия. . В качестве оценки
. В качестве оценки  . Проверим, насколько хороша оценка
. Проверим, насколько хороша оценка  :
: Вывод:
Вывод:  , зависящей от
, зависящей от  неизвестных параметров. Необходимо найти оценки
неизвестных параметров. Необходимо найти оценки  .
.  при больших
при больших  . Более того, можно рассматривать
. Более того, можно рассматривать  как оценку
как оценку  при каждом фиксированном значении
при каждом фиксированном значении  . Поскольку
. Поскольку  , то в качестве успеха в случайном испытании примем:
, то в качестве успеха в случайном испытании примем:  .
. , где
, где  - число выборочных значений, меньших
- число выборочных значений, меньших  , т.е. число успехов.
, т.е. число успехов. 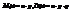 , где
, где  ,
, . Таким образом,
. Таким образом,  . Следовательно,
. Следовательно,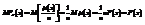
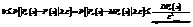
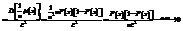 т.к.
т.к.  ,
,