
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Задачи математической статистики. Генеральная совокупность. Выборка.Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов. Вторая задача МС - разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся: а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.; б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен. в) установление статистических зависимостей между случайными событиями, случайными величинами или случайными процессами (регрессионный, корреляционный, дисперсионный, дискриминантный анализ); г) управление случайными процессами; д) планирование эксперимента; О. МС – наука о способах получения, сокращения, хранения и обработки информации. О. Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов. О. Генеральной совокупностью называется совокупность объектов, из которых производится выборка. О. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Предположим, что можем производить измерения случайной величины Х. Допустим, что в n экспериментах результаты измерений Предполагаем, что выполняются следующие две предпосылки: 1. Эксперименты проводятся в одинаковых условиях;  2. Эксперимента проводятся независимо друг от друга. О.Говорят, что результаты n экспериментов О.Говорят, что случайные величины
Если Алгоритм следующий: 1. Разбиваем всю числовую ось на k интервалов (отрезков). 2. Находим 3. Производим расчет вероятностей
5. Рассчитываем 6. По таблице процентных точек распределения X2 находим X2критическое: Проверяем:
О.Функция распределения F(x) случайной величины Х называется теоретической функцией распределения или функцией распределения генеральной совокупности. Как абстрактную, так и конкретную выборку будем обозначать одними и теми же буквами О.Повторной называют выборку, при которой отобранный объект (перед отбором следующего ) возвращается в генеральную совокупность. О.Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида: 1. Отбор не требующий разбиения (расчленения) генеральной совокупности на части. а) простой случайный бесповторный отбор; б) простой случайный повторный отбор. 2. Отбор, при котором генеральная совокупность разбивается на части. а) типический отбор; б) механический отбор; в) серийный отбор. О.Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. О. Типическим называют отбор, при котором объекты выбираются не из всей генеральной совокупности, а из каждой ее “типической” части. О. Механическим называют отбор, при котором генеральную совокупность “механически” делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект. Замечание: Необходимо отметить, что иногда механический отбор может не обеспечить репрезентативность выборки. Например, если замена резца в станке проводится сразу после отбора каждой двадцатой детали, то обратными окажутся все детали, обточенные затупленными резцами. В таком случае можно устранить совпадение ритма отбора с ритмом замены резца. О.Серийным называют отбор, при котором объекты отбираются из генеральной совокупности не по одному, а “сериями”, которые подвергаются сплошному обследованию. На практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы. Например, иногда разбивают генеральную совокупность на серии одинакового объема, затем простым случайным отбором отбирают несколько серий и, наконец, из каждой серии простым случайным отбором извлекают отдельные объекты.
cov(X,Y)=M[(X-MX)(Y-MY)]; cov(X,Y)≈
нормальном распределении). Если
График плотности отношения Фишера.
гипотезу H0: r = 0. При этом предположении Перейдем к противоположному событию:
3.
4. Предположим, что (X,Y)- непрерывный случайный вектор с плотностью p(x,y) О. Условной плотностью вероятности случайной величины X при условии, что X=x называется О. Условным математическим ожиданием случайной величины Y при условии, что X=x называется число: О. Условным математическим ожиданием величины X при условии, что Y=y называется число Обозначим через Все свойства условного математического ожидания, доказанные для дискретных случайных величин, остаются справедливыми и для непрерывных случайных величин.
Линии регрессии:
Коэффициент корреляции: r‹0 ó r<0 ó Линии регрессии совпадут ó |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 193. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
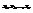 - некоторые числа.
- некоторые числа. образуют абстрактную выборку объема n, если они независимы и одинаково распределены.
образуют абстрактную выборку объема n, если они независимы и одинаково распределены. . Задаем уровень значимости
. Задаем уровень значимости  .
.  ,
,  (% точка распределения X2).
(% точка распределения X2).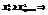 гипотеза H0 отвергается. Если
гипотеза H0 отвергается. Если  H0 согласуется с экспериментальными данными.
H0 согласуется с экспериментальными данными.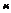
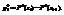


 - H0 – отвергается;
- H0 – отвергается;  - H0 – согласуется с экспериментальными данными.
- H0 – согласуется с экспериментальными данными.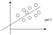
 Если же точки расположены как на рис.6, то строят параболическую регрессию и уравнение вида параболы. Обозначим а=МХ, в=МУ,
Если же точки расположены как на рис.6, то строят параболическую регрессию и уравнение вида параболы. Обозначим а=МХ, в=МУ,  =DX,
=DX,  =DY, r=
=DY, r=  . Т.к. наши параметры неизвестны, то вместо них логично взять их оценки:
. Т.к. наши параметры неизвестны, то вместо них логично взять их оценки:  ,
,  ,
,  ;
;  ;
; . Коэффициент корреляции r=
. Коэффициент корреляции r=  Подставляя в уравнение линейной регрессии оценки, получаем:
Подставляя в уравнение линейной регрессии оценки, получаем: -выборочное ур-е линейной регрессии Y на X.
-выборочное ур-е линейной регрессии Y на X. - выборочное ур-е линейной регрессии X на Y.
- выборочное ур-е линейной регрессии X на Y. . Критическая область будет находиться из следующего условия
. Критическая область будет находиться из следующего условия  , здесь
, здесь 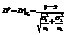 . Если
. Если  , то H0 отвергается; если
, то H0 отвергается; если  , то H0 согласуется с экспериментальными данными.
, то H0 согласуется с экспериментальными данными.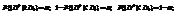
 т.к.
т.к. 

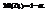
 находим D0 по таблице функции Лапласа.
находим D0 по таблице функции Лапласа.

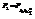 -% точка F-распределения (Фишера).
-% точка F-распределения (Фишера).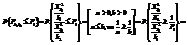

 - процентная точка F – распределения.
- процентная точка F – распределения.  .
.  H0 отвергается.
H0 отвергается.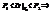 H-0 согласуется с экспериментальными данными.
H-0 согласуется с экспериментальными данными. По лемме о нормальном распределении
По лемме о нормальном распределении  . Критическая область выбирается из:
. Критическая область выбирается из:  Задаем уровень значимости
Задаем уровень значимости 
 Поскольку
Поскольку  то
то  , т.е. t находится по таблице функции Лапласа. Если
, т.е. t находится по таблице функции Лапласа. Если  , то гипотеза Ho отвергается. Если
, то гипотеза Ho отвергается. Если  , то гипотеза H0 согласуется с экспериментальными данными.
, то гипотеза H0 согласуется с экспериментальными данными.



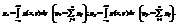
 . Условной плотностью вероятности случайной величины X при условии, что Y=y называется
. Условной плотностью вероятности случайной величины X при условии, что Y=y называется  . Как известно, обычное математическое ожидание
. Как известно, обычное математическое ожидание 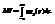
 .
.
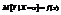 , тогда случайная величина f(X) называется условным математическим ожиданием случайной величины Y при условии X. Обозначается
, тогда случайная величина f(X) называется условным математическим ожиданием случайной величины Y при условии X. Обозначается  , т.е.
, т.е. 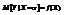 .
.
 ,
, 

 <0,
<0,  <0; r>0ó
<0; r>0ó  и
и  – тупые углы; r>0 ó
– тупые углы; r>0 ó  ó
ó  ó
ó  . Чем меньше угол β , тем точнее прогноз, который даёт линейная регрессия.
. Чем меньше угол β , тем точнее прогноз, который даёт линейная регрессия.