
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Теорема Чебышева и ее смысл.Теорема. Если дисперсии n независимых случайных величин
Или
☺ По условию Получим неравенство Чебышева в форме Найдем математическое ожидание М(Х) и оценку дисперсии D(Х):
(Здесь использованы свойства математического ожидания и дисперсии и, в частности, то, что случайные величины Запишем неравенство
Т.к. по доказанному Следовательно. в пределе при n → ∞ величина Подчеркнем смысл теоремы Чебышева. При большом числе n случайных величин практически достоверно, что их средняя величина случайная, как угодно мало отличается от неслучайной величины, т.е. практически перестает быть случайной. Следствие. Если независимые случайные величины
Или
Теорема Бернулли и ее смысл. Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.  Теорема. Частность события в n повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:
Или ☺ Заключение теоремы непосредственно вытекает из неравенства Чебышева для частости события Смысл теоремы Бернулли состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частность (или статистическая вероятность) события m/n - величина случайная, как угодно мало отличается от неслучайной величины р - вероятности события, т.е. практически перестает быть случайной. Теорема Бернулли является следствием теоремы Чебышева. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 227. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняяарифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий
ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняяарифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий  , т.е.
, т.е.

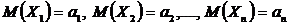 ,
,  , где С - постоянное число.
, где С - постоянное число. для средней арифметической случайных величин, т.е. для
для средней арифметической случайных величин, т.е. для 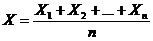 .
.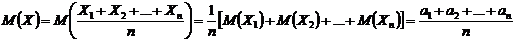 ;
; .
. независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.)
независимы, а следовательно, дисперсия их суммы равна сумме дисперсий.) для случайной величины
для случайной величины  :
: .
. , то
, то  ,
,
 стремится к нулю, и получим доказываемую формулу. ☻
стремится к нулю, и получим доказываемую формулу. ☻ имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то:
имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной, то: ,
,



 при n → ∞. ☻
при n → ∞. ☻