
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Следствие из интегральной теоремы Муавра Лапласа.Пусть выполнили условие применимости интегральной теоремы М.Лапласа, тогда: 1)Вер-ть того, что число m наступлений события А в n испытаниях отличается от величины np не более, чем на эпсило (E) (по абсолютной величине) вычисл. По след. ф-ле: 2)Вер-ть того что частость (доля) m/n наступлений событий А в n испытаниях отличается от вер-ти р не более чем на D (по абсолютной величине) вычисл. По след. ф-ле: 31. Сформулируйте теорему Пуассона. Как найти параметр λ? Если вероятность р наступления события А в каждом испытании стремится к нулю (р → 0) при неограниченном увеличении числа n испытаний (n → 0), причем произведение nр стремится к постоянному числу λ(nр → λ), то вероятность Рm,n того, что событие А появится m раз в n независимых испытаниях, удовлетворяет предельному равенству:
Т.е. условие теоремы Пуассона р → 0 при n → ∞, так что nр → λ, противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании р = const. Однако, если вероятность р - постоянна и мала, число испытаний n - велико и число λ = nр - незначительно (будем полагать, что λ = np ≤ 10), то из предельного равенства
В качестве оценки неизвестного параметра λ по n наблюдённым значениям независимых случайных величин А1,..., Аn используется их арифметическое среднее А = (А1 +... + Аn)/n, поскольку эта оценка лишена систсматической ошибки и её квадратичное отклонение минимально. (λ — положительный параметр)  СЛУЧАЙНЫЕ ВЕЛИЧИНЫ Опрделение сучайной величиы. Примеры непрерывных и дискретных случайных величин. Опр.: Случайной величиной называется переменная, кот. в рез-те испытания принимает то или иное числовое значение. Опр. Случайная величина назыв. дискретной, если число её возможных значений конечно или счётно (множество счетное, если его можно перенумеровать натур.альными . числами). Опред.: Случ. величина назыв. непрерывной, если её значение полностью заполняют некоторый интервал. Пр1)число попаданий в мишень, (количество учеников в классеßдискретная случ. величина; Пр2) рост человека, рост дереваßнепрерывная случ. величина.; Закон распределения дискретной случайной величины. Законом распр. ДСВ (Х) наз. соответствие между знач. случ. величины и вероятностями, с кот. она принимает эти знач-я, причем оассм. все возможные значения этой величины (СВ).записывают в виде таблиц
х1<x2<…<xn, т.к. это все возможные знач. ДСВ(Х), то соб. Х=х1, Х=х2…Х=хn, то соб. образ. полную группу (сис-му). р1+р2+…+рn=1эта ф-ла прим. для контроля правильности построения закона распр. ∑Pn=1. |
||||||||||||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 249. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



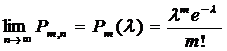
 вытекает приближенная формула Пуассона:
вытекает приближенная формула Пуассона: .Cобытия, для которых применима формула Пуассона, называют редкимитак как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).
.Cобытия, для которых применима формула Пуассона, называют редкимитак как вероятность их осуществления очень мала (обычно порядка 0,001-0,0001).