
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Запишит формулу Бейеса. Какое ее предназначение?Следствием теоремы умножения и формулы полной вероятности является формула Байеса. Она применяется, когда событие F, которое может появиться только с одной из гипотез А1,А2,…,Аn образующих полную группу событий, произошло и необходимо произвести количественную переоценку априорных вероятностей этих гипотез P(A1), Р(А2),..., Р(Аn), известных о испытания, Т.е. надо найти апостериорные (получаемые после проведения испытания) условные вероятности гипотез PF(A1),PF(А2),...,РF(Аn). □ Для получения искомой формулы запишем теорему умножения вероятностей событий F и Аi в двух формах: откуда или с учетом формулы полной вероятности: Значение формулы Байеса состоит в том, что при наступлении события Р, т.е. по мере получения новой информации, мы можем проверять и корректировать выдвинутые до испытания гипотезы. Такой подход, называемый байесовским,дает возможность корректировать управленческие решения в эк-ке, оценки неизвестных параметров распределения изучаемых признаков в статистическом анализе. ПОВТОРЕНИЕ НЕЗАВИСИМЫХ ИСПЫТАНИЙ Запишите формлу Бернулли. Какое ее предназначение? Теорема. Если вероятность р наступления соб. А в каждом испытании постоянна, то вероятность Рm,n того, что соб. А наступит m раз в n независимых испытаниях, равна  При решении вероятностных задач часто приходится сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент еще называется схемой повторных независимых испытаний или схемой Бернулли. Примеры повторных испытаний: 1) многократное извлечение из урны одного шара при условии, что вынутый шар после регистрации его цвета кладется обратно в урну; 2) повторение одним стрелком выстрелов по одной и той же мишени при условии, что вероятность удачного попадания при каждом выстреле принимается одинаковой |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 210. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,
 . ■
. ■ , q=1-p. Док-во: Пусть Ai и Āi - соответственно появление и непоявление соб. А в i-м испытании (i=1,2…n), а Bm – соб-е, состоящее в том, что в n независимых испытаниях соб. А появилось m раз. Представим событие Вm через элементарные события Ai. Наприм n=3, m=2: В2=А1А2Ā+А1ĀА3+ ĀА2А3. В общем виде: Bm=А1А2…AmĀm+1+A1Ā2A3…Ān-1An+…+Ā1Ā2… Ān-mĀn-m+1, т.е. кажд вариант появл-я соб. Вm состоит из m появлений соб. А и n-m соб. Ā с разн индексами. Число всех комбинаций = числу способов выбора из n испытаний m, в котор соб-е А произошло, т.е. числу сочетаний
, q=1-p. Док-во: Пусть Ai и Āi - соответственно появление и непоявление соб. А в i-м испытании (i=1,2…n), а Bm – соб-е, состоящее в том, что в n независимых испытаниях соб. А появилось m раз. Представим событие Вm через элементарные события Ai. Наприм n=3, m=2: В2=А1А2Ā+А1ĀА3+ ĀА2А3. В общем виде: Bm=А1А2…AmĀm+1+A1Ā2A3…Ān-1An+…+Ā1Ā2… Ān-mĀn-m+1, т.е. кажд вариант появл-я соб. Вm состоит из m появлений соб. А и n-m соб. Ā с разн индексами. Число всех комбинаций = числу способов выбора из n испытаний m, в котор соб-е А произошло, т.е. числу сочетаний 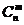 . Вер-сть каждой такой комбинации (кажд варианта появл-я соб. Вm) по теор умножения для независ-х соб-й =pmqn-m, т.к. р(Аi)=p, p(Āi)=q, q=1,2…n. В связи с тем, что комбинации между собой несовместны, по теор сложения вероятностей получим: Pm,n=(P(Bm)=pmqn-m+…+ pmqn-m) –складываем раз = pmqn-m.
. Вер-сть каждой такой комбинации (кажд варианта появл-я соб. Вm) по теор умножения для независ-х соб-й =pmqn-m, т.к. р(Аi)=p, p(Āi)=q, q=1,2…n. В связи с тем, что комбинации между собой несовместны, по теор сложения вероятностей получим: Pm,n=(P(Bm)=pmqn-m+…+ pmqn-m) –складываем раз = pmqn-m.