
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Функция одного случайного аргумента.Если каждому значению случайной величины X соответствует единственное значение случайной величины Y, то Y называют функцией одного случайного аргумента X.
Нахождение распределения функции по известному распределению аргумента. X — дискретная случайная величина. Если различным возможным значениям аргумента X соответствуют различные значения функции Y, то вероятности соответствующих значений X и Y между собой равны. Если различным возможным значениям аргумента X соответствуют значения Y, среди которых есть равные между собой, то следует складывать вероятности повторяющихся значений Y. X — непрерывная случайная величина. Если
Математическое ожидание функции одного случайного аргумента. X — дискретная случайная величина.
X — непрерывная случайная величина.
Функция двух случайных аргументов. Если каждой паре случайных аргументов X и Y соответствует одно возможное значение случайной величины Z, то говорят, что задана функция двух случайных аргументов:
Распределение Пусть
распределена по закону Функция распределения:
Распределение Стьюдента Пусть Z — нормальная случайная величина, причем
 имеет распределение, которое называют t-распределением, или распределением Стьюдента с k степенями свободы.
Показательное распределение Показательным называют распределение вероятностей, которое описывается дифференциальной функцией
Где Примером непрерывной случайной величины, распределенной по показательному закону, может служить время между появлениями двух последовательных событий простейшего потока. Найдем интегральную функцию показательного распределения.
Вероятность попадания в заданный интервал показательно распределенной случайной величины
Числовые характеристики показательного распределения. Пусть непрерывная случайная величина X, распределена по показательному закону:
Найдем математическое ожидание
Получаем, что Таким образом, математическое ожидание показательного распределения равно обратной величине параметра Найдем дисперсию
Получаем, что
Математическое ожидание и среднее квадратическое отклонение показательного распределения равны между собой.
Система двух случайных величин Будем обозначать через Различают дискретные (составляющие дискретны) и непрерывные (составляющие непрерывны) многомерные системы случайных величин. |
||
|
Последнее изменение этой страницы: 2018-05-27; просмотров: 231. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 дифференцируемая, строго возрастающая или строго убывающая функция, обратная функция которой
дифференцируемая, строго возрастающая или строго убывающая функция, обратная функция которой 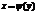 , то дифференциальная функция
, то дифференциальная функция  случайной величины Y находится по равенству:
случайной величины Y находится по равенству:


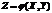
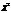
 — независимые нормально распределенные случайные величины (
— независимые нормально распределенные случайные величины (  ). Тогда сумма квадратов этих величин
). Тогда сумма квадратов этих величин
 степенями свободы.
степенями свободы.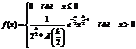 , где
, где 
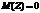 ,
,  , a V — независимая от Z величина, которая распределена по закону
, a V — независимая от Z величина, которая распределена по закону 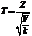

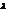 — постоянная положительная величина.
— постоянная положительная величина.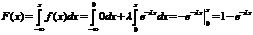
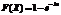
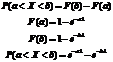



 .
.


 двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой). Обе величины X и Y, рассматриваемые одновременно образуют систему двух случайных величин.
двумерную случайную величину. Каждую из величин X и Y называют составляющей (компонентой). Обе величины X и Y, рассматриваемые одновременно образуют систему двух случайных величин.