
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Представление синусоидальных величин комплексными числами.Для того чтобы представить заданную в тригонометрической форме синусоидальную величину
с начальной фазой j комплексным числом, проведем на комплексной плоскости из начала координат под углом j к оси действительных величин вектор, длина которого в масштабе построения равна амплитуде Am исходной синусоидальной величины.
Конец этого вектора находится в точке, которой соответствует определенное комплексное число - комплексная амплитуда синусоидальной величины:
При увеличении во времени фазы (wt + j) синусоидальной величины угол между вектором и осью действительных величин растет, то есть получается вращающийся вектор
Вектор на комплексной плоскости, длина которого в масштабе построения равна действующему значению синусоидальной величины, и соответствующее комплексное число называются комплексным действующим значением синусоидальной величины:
Применяется три формы записи комплексного значения синусоидальной величины: 1) показательная
2) тригонометрическая
3) алгебраическая
где При анализе цепей синусоидального тока применяют главным образом комплексные действующие значения синусоидальных величин. Например, синусоидальному току
соответствует комплексное значение тока
Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элемента
Зависимости между токами и напряжениями резистивных, индуктивных и емкостных элементов определяются происходящими в них физическими процессами. Математическое описание физических явлений для каждого из этих элементов зависит от выбранного способа представления синусоидальных величин. 
Резистивный элемент. Выберем положительное направление синусоидального тока.
Для мгновенных значений напряжения и тока справедливо соотношение, определяемое законом Ома:
или
где амплитуды тока и напряжения связаны соотношением
а начальные фазы
то есть ток и напряжение в резистивном элементе изменяются синфазно – совпадают по фазе (см. рисунок). Разделив правую и левую части выражения (1) на
Представим теперь синусоидальные ток и напряжение резистивного элемента соответствующими комплексными значениями:
Так как
Соотношение между током и напряжением наглядно может быть представлено на векторной диаграмме тока и напряжения, построенной в выбранном масштабе на комплексной плоскости:
Индуктивный элемент. Если в индуктивном элементе ток синусоидальный:
то по закону электромагнитной индукции на индуктивном элементе появится напряжение:
где амплитуды напряжения и тока связаны соотношением
а их начальные фазы:
Разделив правую и левую части выражения (2) на
где xL = wL [Ом] – сопротивление индуктивного элемента.
Величину xL также называют индуктивным сопротивлением, а обратную ей величину bL =1/xL = 1/wL – индуктивной проводимостью. Значения величин xL и bL являются параметрами индуктивных элементов цепей синусоидального тока. Индуктивное сопротивление пропорционально угловой частоте w синусоидального тока и при постоянном токе (w = 0) оно равно нулю. По этой причине многие аппараты и приборы не могут включаться в цепь постоянного тока, так как их сопротивление в этом случае очень мало. Представим синусоидальные ток
На векторной диаграмме показано, что вектор комплексного значения тока
или
Входящая в это выражение величина jwL = jxL называется комплексным сопротивлением индуктивного элемента, а обратная ей величина 1/jwL = -jbL – комплексной проводимостью индуктивного элемента. Емкостной элемент. Если напряжение между выводамиемкостного элемента изменяется по синусоидальному закону:
то синусоидальный ток
где амплитуды связаны соотношением
а начальные фазы
Разделив правую и левую части выражения (3) на
где
В противоположность индуктивному сопротивлению емкостное сопротивление уменьшается с увеличением частоты синусоидального тока. При постоянном напряжении емкостное сопротивление бесконечно велико. На рисунке показан график мгновенных значений синусоидальных напряжения и тока для емкостного элемента. Из рисунка видно, что синусоидальное напряжение Представим синусоидальные ток
На векторной диаграмме показано, что вектор комплексного значения напряжения
Величина 1/jwС = -jxС называется комплексным сопротивлением емкостного элемента, а обратная ей величина jwС = jbС – комплексной проводимостью емкостного элемента. |
||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 378. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |



 .
. .
.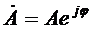 ,
,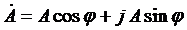 ,
, ,
,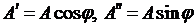 – действительная и мнимая составляющие комплексного значения синусоидальной величины;
– действительная и мнимая составляющие комплексного значения синусоидальной величины;  .
.
 .
.

 ,
, ,
, , (1)
, (1) ,
, , получим соотношение для действующих значений:
, получим соотношение для действующих значений:

 .
. , то закон Ома в комплексной форме имеет следующий вид:
, то закон Ома в комплексной форме имеет следующий вид: .
.
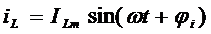 ,
, ,
, , (2)
, (2) .
. ,
,
 и напряжение
и напряжение  соответствующими комплексными значениями:
соответствующими комплексными значениями: .
.
 отстает по фазе от вектора комплексного значения напряжения
отстает по фазе от вектора комплексного значения напряжения  на угол
на угол 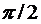 , что соответствует сдвигу фаз j = p/2. Закон Ома в комплексной форме для индуктивного элемента имеет вид:
, что соответствует сдвигу фаз j = p/2. Закон Ома в комплексной форме для индуктивного элемента имеет вид: ,
,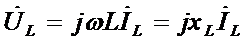 .
. ,
, ,
, , (3)
, (3)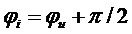 .
. ,
, – емкостное сопротивление,
– емкостное сопротивление,  – емкостная проводимость.
– емкостная проводимость.
 отстает по фазе от синусоидального тока
отстает по фазе от синусоидального тока 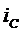 на угол
на угол  , то есть сдвиг по фазе между напряжением и током
, то есть сдвиг по фазе между напряжением и током  .
. и напряжение
и напряжение  емкостного элемента соответствующими комплексными значениями:
емкостного элемента соответствующими комплексными значениями: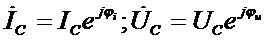 .
.
 отстает по фазе от вектора комплексного значения тока
отстает по фазе от вектора комплексного значения тока  напряжения на угол
напряжения на угол  .
.