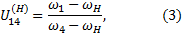Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Кинематический анализ зубчатых механизмов
Цель работы: изучение кинематики зубчатых передач. Определение передаточных отношений зубчатых механизмов. Объект исследования: модели механизмов. Передаточным отношением зубчатого механизма называется отношение угловых скоростей w ведущего колеса wj и ведомого wk. Если j – ведущее колесо, а k – ведомое, то
Если движение передается от k-го колеса к j-ому, то
Если угловая скорость ведущего колеса больше, чем угловая скорость ведомого (U>1), то такой механизм называется редуктором; в противном случае – мультипликатором. На кинематических схемах зубчатые колеса принято изображать в виде окружностей, которые касаются друг друга. Эти окружности называют начальными. Одноступенчатые зубчатые механизмы состоят из двух колес и стойки (рис. 1). Передаточное отношение может быть выражено через другие параметры колес:
где Zk, Zj – числа зубьев k и j колес соответственно: знак «+» ставится, если колеса вращаются в одном направлении (внутреннее зацепление), в противном случае – «–» (внешнее зацепление). Передаточное отношение одноступенчатой червячной передачи при ведущем червяке (под Z следует понимать число заходов червяка) определяется по предыдущей формуле. Направление вращения ведомого звена следует определять по правилу винта и гайки.
Рис. 1
Число заходов червяка определяется подсчетом количества витков резьбы на его торце.  Для механизмов, имеющих кроме ведомого и ведущего еще несколько промежуточных колес (рис. 2), передаточное отношение от ведущего (первого) к ведомому (n-му) колесу определяется формулой
Такой ряд колес применяется для передачи движения между валами, находящимися на большом удалении друг от друга или при необходимости воспроизведения передаточного отношения определенного знака.
Рис. 2
Для получения большого передаточного отношения применяется ступенчатый ряд колес, в котором, в отличие от последовательного ряда колес, колеса жестко соединены между собой осью и представляют собой одно звено (рис. 3). В этом случае передаточное отношение равно произведению передаточных отношений отдельных ступеней:
Рис. 3
Опытным путем передаточное отношение любой зубчатой передачи от колеса 1 к колесу n определяется поворотом входного колеса на 360° и замером угла φn поворота выходного звена, тогда
Знак определяется во направленно вращения выходного звена.
Порядок выполнения работы
1. Ознакомиться с устройством исследуемых механизмов. 2. Составить кинематическую схему исследуемого механизма 3. Заполнить таблицу 1, в которой число столбцов равно числу исследуемых механизмов.
Таблица 1
Контрольные вопросы
1. Что такое одноступенчатая передача? Что такое многоступенчатая передача? 2. Как определить знак передаточного отношения? 3. В каком случае применяется последовательный ряд колес и в каком ступенчатый? 4. Как вычислить передаточное отношение ступенчатого и последовательного рядов колес? 5. С какой целью определяется передаточные отношения зубчатых механизмов?
Лабораторная работа №26 Кинематический анализ планетарных и дифференциальных механизмов
Цель работы: ознакомление с кинематикой планетарных и дифференциальных механизмов и определение их передаточных отношений практическим и теоретическим методом. Объект исследования: модели планетарных и дифференциальных механизмов. В предыдущей лабораторной работе были изучены зубчатые механизмы с неподвижными осями вращения. Отличительная особенность планетарных и дифференциальных механизмов – наличие зубчатых колес с подвижной осью вращения. На рис.1 изображен планетарный механизм. У него колесо 4 неподвижно, общая ось колес 2 и 2¢ вращается вместе с водилом Н вокруг колес 1 и 4, называемых солнечными. Колеса 2 и 2¢ называются сателлитами, а механизм – планетарным по аналогии с солнечной системой, в которой планеты, совершая оборот вокруг Солнца, вращаются также вокруг собственной оси. У планетарного механизма степень подвижности равна единице. Если освободить колесо 4, то мы получим дифференциальный механизм, имеющий две степени свободы. Для определения передаточного отношения планетарных механизмов применяется метод инверсии. В данном случае этот метод эквивалентен закреплению водила и освобождению неподвижного колеса.
Рис. 1
При этом мы получаем зубчатую передачу с неподвижными осями, передаточное отношение которой может быть определено по методике, изложенной в предыдущей лабораторной работе. На рис. 2 представлена схема механизма в обращенном движении. Передаточное отношение планетарного механизма обозначается буквой U, где верхний индекс указывает на неподвижное звено, а нижний индекс указывает номера входного и выходного звеньев. Для механизма на рис. 1, имеющего в качестве входного звена колесо 1, в качестве выходного водило Н, при закрепленном колесе 4. Передаточное отношение обозначается
Рис. 2
Передаточное отношение рассматриваемого планетарного механизма определяется по формуле Виллиса
В общем случае передаточное отношение от i-го колеса планетарного механизма к водилу при неподвижном j-ом колесе определяется формулой
Передаточное отношение дифференциального механизма (рис. 3) определяется из формулы передаточного отношения обращенного механизма
из которой следует, что дифференциальный механизм не имеет определенного передаточного отношения, если одно входное звено имеет определенную угловую скорость. Только при заданной угловой скорости двух входных звеньев (например, 1 и Н) передаточное отношение становится определенным.
Рис. 3
Определение передаточного отношения опытным путем. В планетарном механизме (рис. 1) поворачиваем входное звено (водило Н) на угол φН=360°, определяем угол φ1 поворота выходного звена (колеса 1), тогда передаточное отношение исследуемого механизма равно
Знак передаточного отношения определяется визуально.
Порядок выполнения работы
1. Ознакомиться с устройством исследуемых механизмов. 2. Заполнить приведенные ниже табл. 1, вычертив схемы исследуемого и обращенного механизмов.
Таблица 1
Контрольные вопросы
1. В чем отличие планетарного механизма и зубчатой передачи? 2. В чем отличие планетарного и дифференциального механизмов? 3. Почему дифференциальный механизм не обладает определенным передаточным отношением? 4. Для чего применяется метод инверсии при определении передаточного отношения планетарного механизма? 5. Каким образом можно получить планетарный механизм из дифференциального?
Лабораторная работа №27 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-05-10; просмотров: 467. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
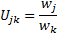
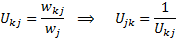





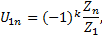

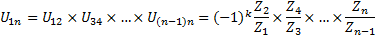



 , а для обращенного механизма –
, а для обращенного механизма –  .
.