
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
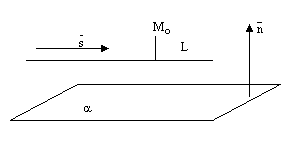
Билет 9. Взаимное расположение прямой и плоскости в пространстве.Прямая может лежать на данной плоскости, быть параллельна данной плоскости или пересекать ее в одной точке, см. следующие рисунки.
рис.6. рис.7. рис.8.
Теорема. Пусть плоскость
а прямая L задана каноническими уравнениями
или параметрическими уравнениями
в которых координаты направляющего вектора прямой L. Тогда: 1) если
2) если 3) если Доказательство. Условие Если  Если Теорема доказана.
Билет 11.Случаи взаимного расположения плоскостей:
Свойства параллельных плоскостей:
Определение расстояния между точкой и плоскостью, прямой и плоскостью, между плоскостями и скрещивающимися прямыми Определение расстояния между: 1 — точкой и плоскостью; 2 — прямой и плоскостью; 3 — плоскостями; 4 — скрещивающимися прямыми рассматривается совместно, так как алгоритм решения для всех этих задач по существу одинаков и состоит из геометрических построений, которые нужно выполнить для определения расстояния между заданными точкой А и плоскостью а. Если и есть какое-то различие, то оно состоит лишь в том, что в случаях 2 и 3 прежде чем приступить к решению задачи, следует на прямой m (случай 2) или плоскости /3 (случай 3) отметить произвольную точку А. При определении расстояния между скрещивающимися прямыми предварительно заключаем их в параллельные плоскости а и /3 с последующим определением расстояния между этими плоскостями.
Параллельность двух плоскостей Определение. Две плоскости называются параллельными , если они не имеют общих точек. Если плоскость α параллельна каждой из двух пересекающихся прямых, лежащих в другой плоскости β, то эти плоскости параллельны. Если две параллельные плоскости пересечены третьей, то она оставляет на этих плоскостях параллельные следы. Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну. ОтДва угла с соответственно параллельными и одинаково направленными сторонами равны и лежат в параллельных плоскостях. резки параллельных прямых, ограниченные двумя параллельными плоскостями, равны. нахождение расстояния между двумя параллельными прямыми 1) Запишите уравнение плоскости, перпендикулярной заданным прямым, её нормальным вектором является направляющий вектор любой из заданных прямых, и возьмите точку, например, первой прямой. 2) найдите точку пересечения второй прямой и найденной плоскости, для чего уравнение прямой придётся переводить в параметрический вид. 3) найдите расстояние между найденной точкой пересечения и точкой первой прямой, через которую проводили плоскость. Это и будет искомое расстояние. 12).Признак перпендикулярности плоскостей факт Две плоскости называются перпендикулярными (взаимно перпендикулярными), если они пересекаются под прямым углом, т.е. все четыре двугранных угла, образованные при пересечении этих плоскостей --- прямые. Справедлива следующая теорема (необходимое и достаточное условие перпендикулярности плоскостей). Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через прямую, перпендикулярную другой. Одна из частей этой теоремы (достаточность) есть признак перпендикулярности двух плоскостей. |
||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 364. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||


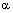 задана общим уравнением
задана общим уравнением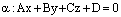 ,
,
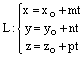 ,
,  ,
, – координаты нормального вектора плоскости
– координаты нормального вектора плоскости  – координаты произвольной фиксированной точки прямой L,
– координаты произвольной фиксированной точки прямой L,  –
–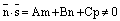 , то прямая L пересекает плоскость
, то прямая L пересекает плоскость  можно найти из системы уравнений
можно найти из системы уравнений ; (7)
; (7)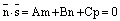 и
и  , то прямая лежит на плоскости;
, то прямая лежит на плоскости; , то прямая параллельна плоскости.
, то прямая параллельна плоскости. говорит о том, что векторы
говорит о том, что векторы  и
и  не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки.
не ортогональны, а значит прямая не параллельна плоскости и не лежит в плоскости, а значит пересекает ее в некоторой точке М. Координаты точки М удовлетворяют как уравнению плоскости, так и уравнениям прямой, т.е. системе (7). Решаем первое уравнение системы (7) относительно неизвестной t и затем, подставляя найденное значение t в остальные уравнения системы, находим координаты искомой точки. , то это означает, что
, то это означает, что  . А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка
. А такое возможно лишь тогда, когда прямая лежит на плоскости или параллельна ей. Если прямая лежит на плоскости, то любая точка прямой является точкой плоскости и координаты любой точки прямой удовлетворяют уравнению плоскости. Поэтому достаточно проверить, лежит ли на плоскости точка  – лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
– лежит на плоскости, а это означает, что и сама прямая лежит на плоскости.
 . Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости
. Тогда прямая а проходит через точку А пересечения прямых b и c. Докажем, что прямая а перпендикулярна плоскости  рис. 24 плоскости а и в пересекаются
рис. 24 плоскости а и в пересекаются плоскости а и в параллельны
плоскости а и в параллельны 1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
1. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. 2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.
2. Отрезки параллельных прямых, заключённые между параллельными плоскостями, равны.