
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Синус, косинус и тангенс суммы и разности двух угловСтр 1 из 14Следующая ⇒ Билет 1. Радианная мера угла. Радианная мера угла. Что такое радиан? В основе определения радиана - всё равно окружность. Угол в 1 радиан, это угол, который вырезает из окружности дугу, длина которой (L) равна длине радиуса (R). Смотрим картинки. Действительно, в 180° градусах укладывается 3,1415926... радиан. Как вы сами понимаете, всё время писать 3,1415926... неудобно. Поэтому вместо этого бесконечного числа всегда пишут просто:
Или точное равенство:
! Если в 3,14 радианах 180° градусов, то в 1 радиане в 3,14 раз меньше! То есть, мы делим первое уравнение (формула - это тоже уравнение!) на 3,14:
Это соотношение полезно запомнить В одном радиане примерно 60°. В тригонометрии очень часто приходится прикидывать, оценивать ситуацию. Вот тут это знание очень помогает. Но главное умение этой темы - перевод градусов в радианы и обратно. Если угол задан в радианах с числом "Пи", всё очень просто. Мы знаем, что "Пи" радиан = 180°. Вот и подставляем вместо "Пи" радиан - 180°. Получаем угол в градусах. Сокращаем, что сокращается, и ответ готов. Например, нам нужно выяснить, сколько градусов в угле "Пи"/2 радиан? Вот и пишем:
Тригонометрические функции
Основные тригонометрические тождества  o sin² α + cos² α = 1 o tg α · ctg α = 1 o tg α = sin α ÷ cos α o ctg α = cos α ÷ sin α o 1 + tg² α = 1 ÷ cos² α o 1 + ctg² α = 1 ÷ sin² α
o Преобразование тригонометрические выражений - это процесс упрощения выражений с применением основных тригонометрических формул: o o В разделе преобразование тригонометрических выражений на базовом уровне требуется так же знание формул приведения. o o o Знак приводимой и приведенной функции одинаков.
Билет 2 Синус, косинус и тангенс суммы и разности двух углов Формулы суммы углов (формулы сложения аргументов) для функций косинуса и синуса выглядят следующим образом:
Формулы приведения
В тождественных преобразованиях тригонометрических выражений могут быть использованы следующие алгебраические приемы: добавление и вычитание одинаковых слагаемых; вынесение общего множителя за скобки; умножение и деление на одну и ту же величину; применение формул сокращенного умножения; выделение полного квадрата; разложение квадратного трехчлена на множители; введение новых переменных с целью упрощения преобразований. При преобразованиях тригонометрических выражений, содержащих дроби, можно использовать свойства пропорции, сокращение дробей или приведение дробей к общему знаменателю. Кроме того, можно пользоваться выделением целой части дроби, умножением числителя и знаменателя дроби на одинаковую величину, а так же по возможности учитывать однородность числителя или знаменателя. При необходимости можно представлять дробь в виде суммы или разности нескольких более простых дробей. Кроме того, применяя все необходимые методы преобразования тригонометрических выражений, необходимо постоянно учитывать облась допустимых значений преобразуемых выражений. Рассмотрим несколько примеров. Пример 1. Вычислить А = (sin (2x – π) · cos (3π – x) + sin (2x – 9π/2) · cos (x + π/2))2+ (cos (x – π/2) · cos (2x – 7π/2) + Решение. Из формул приведения следует: sin (2x – π) = -sin 2x; cos (3π – x) = -cos x; sin (2x – 9π/2) = -cos 2x; cos (x + π/2) = -sin x; cos (x – π/2) = sin x; cos (2x – 7π/2) = -sin 2x; sin (3π/2 – x) = -cos x; sin (2x – 5π/2) = -cos 2x. Откуда в силу формул сложения аргументов и основного тригонометрического тождества получаем А = (sin 2x · cos x + cos 2x · sin x)2 + (-sin x · sin 2x + cos x · cos 2x)2 = sin2 (2x + x) + cos2 (x + 2x) = Ответ: 1. Билет 5. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 1086. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |





 Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.
Это отношение не зависит от выбора треугольника ABC, содержащего угол α, так как все такие треугольники подобны.  Косинус угла — отношение прилежащего катета к гипотенузе:
Косинус угла — отношение прилежащего катета к гипотенузе: 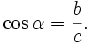 Так как
Так как  синус одного острого угла в треугольнике равна косинусу второго, и наоборот.
синус одного острого угла в треугольнике равна косинусу второго, и наоборот. 
 Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.
Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго, и наоборот.
 , а так же производных от них.
, а так же производных от них. - если n четно (т.е. к α добавляется целое π)
- если n четно (т.е. к α добавляется целое π) - если n нечетно, функция меняется на ко-функцию, все это относится и к tg, ctg.
- если n нечетно, функция меняется на ко-функцию, все это относится и к tg, ctg.