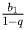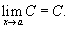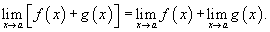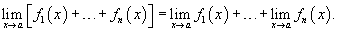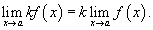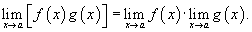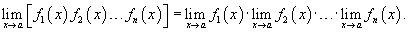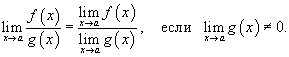Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Операции над последовательностямиНа множестве всех последовательностей элементов множества
Суммой числовых последовательностей Разностью числовых последовательностей Произведением числовых последовательностей Частным числовой последовательности Конечно, арифметические операции могут быть определены не только на множестве числовых последовательностей, но и на любых множествах последовательностей элементов множеств, на которых определены арифметические операции, будь то поля или даже кольца. Подпоследовательность последовательности Иными словами, подпоследовательность получается из последовательности удалением конечного или счётного числа элементов.  Предел последовательности — это объект, к которому члены последовательности приближаются с ростом номера. Так в произвольном топологическом пространстве пределом последовательности называется элемент, в любой окрестности которого лежат все члены последовательности, начиная с некоторого. В частности для числовых последовательностей предел — это число, в любой окрестности которого лежат все члены последовательности начиная с некоторого. Частичный предел последовательности — это предел одной из её подпоследовательностей. У сходящихся числовых последовательностей он всегда совпадает с обычным пределом. Верхний предел последовательности — это наибольшая предельная точка этой последовательности. Нижний предел последовательности — это наименьшая предельная точка этой последовательности. Сумма последовательности. Дана последовательность: 1*2+2*3*4+4*5*6*7+7*8*9*10*11+...{и та до <1000}. Каждое последующее произведение увеличивается на одно число. Посчитать сумму последовательности. Цикл while. Формула суммы всех членов бесконечной геометрической прогрессии Сумма бесконечной геометрической прогрессии со знаменателем q, где |q|<1 , имеет огромное значение в формировании математических знаний. В связи с отсутствием теории пределов в современном школьном курсе алгебры формула суммы бесконечной геометрической прогрессии не доказывается, а поясняется на интуитивном уровне. Поэтому, основным назначением этой формулы в современном школьном курсе стал перевод бесконечной периодической дроби в обыкновенную дробь. Утеряна первоначальная формулировка: если |q|<1 , то при неограниченном возрастании числа n сумма Это число называется суммой бесконечной геометрической прогрессии при |q|<1.
Билет 17. Предел функции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке. Предел функции является обобщением понятия предела последовательности: изначально под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится.
Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят).
В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств.
Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а также описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности».
Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности.
Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Предел фу́нкции — одно из основных понятий математического анализа. Теоремы о пределах 1. Бесконечно большие и бесконечно малые. Функция f(x) стремится к бесконечности при x стремящимся к a, если для любого M > 0 можно указать такое значение d > 0, что для всех x удовлетворяющих неравенству |x-a| < d имеет место неравенство |f(x)| > M.limx® a=Ґ 2. Функция ограниченная при x® a. 3. Функция ограниченная при x® Ґ. 4. Теорема. Если limx® a f(x)=b, то функция f(x) ограниченная при x® a. 5. Бесконечно малые и их свойства. limx® a a(x)=0 Теорема. 1. Если f(x)=b+a, где a - б.м. при x® a, то limx® a f(x)=b и обратно, если limx® a f(x)=b, то можно записать f(x)=b+a(x). Теорема. 2. Если limx® a a(x)=0 и a(x) № 0, то 1/a® Ґ. Теорема. 3. Сумма конечного числа б.м. есть б.м. Теорема. 4. Произведение б.м. на ограниченную функцию есть б.м. 6. Теоремы о пределах. Теорема. 1. Предел суммы есть сумма пределов. Теорема. 2. Предел произведения есть произведение пределов. Теорема. 3. Предел частного есть частное пределов (если знаменатель не обращается в 0). Теорема. 4. Если u(x) Ј z(x) Ј v(x), и limx® a u(x)=limx® a v(x)=b, то limx® a z(x)=b. ("Теорема о двух милиционерах"). 7. Первый замечательный предел. 0.5sin(x) < 0.5x < 0.5tg(x) 8. Второй замечательный предел. Переменная величина при Свойства пределов функцииn® Ґ имеет предел, заключенный между 2 и 3. Свойства пределов функции 1) Предел постоянной величины Предел постоянной величины равен самой постоянной величине:
2) Предел суммы Предел суммы двух функций равен сумме пределов этих функций:
Аналогично предел разности двух функций равен разности пределов этих функций. Расширенное свойство предела суммы: Предел суммы нескольких функций равен сумме пределов этих функций:
Аналогично предел разности нескольких функций равен разности пределов этих функций. 3) Предел произведения функции на постоянную величину Постоянный коэффициэнт можно выносить за знак предела: 4) Предел произведения Предел произведения двух функций равен произведению пределов этих функций:
Расширенное свойство предела произведения Предел произведения нескольких функций равен произведению пределов этих функций:
5) Предел частного Предел частного двух функций равен отношению пределов этих функций при условии, что предел знаменателя не равен нулю:
|
|||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 323. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 можно определить арифметические и другие операции, если таковые определены на множестве
можно определить арифметические и другие операции, если таковые определены на множестве 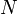 -арная операция
-арная операция 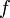 :
:
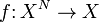 Тогда для элементов
Тогда для элементов 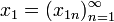 ,
, 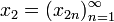 , …,
, …, 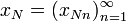 множества всех последовательностей элементов множества
множества всех последовательностей элементов множества 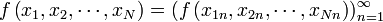
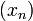 и
и  называется числовая последовательность
называется числовая последовательность 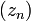 такая, что
такая, что  .
.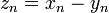 .
.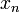 и
и  называется числовая последовательность
называется числовая последовательность 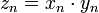 .
.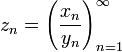 . Если в последовательности
. Если в последовательности 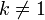 всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность
всё же имеется нулевой элемент, то результат деления на такую последовательность всё равно может быть определён, как последовательность 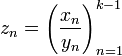 .
.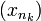 , где
, где 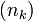 — возрастающая последовательность элементов множества натуральных чисел.
— возрастающая последовательность элементов множества натуральных чисел.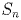 стремится к числу
стремится к числу