
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Учет продольных сил в расчетах сооружений методом перемещений ⇐ ПредыдущаяСтр 8 из 8 Необходимость учета продольных сил при расчете стержневых систем методом перемещений требует особого подхода к определению количества неизвестных в решаемых задачах. При этом формула (19.1) остается справедливой, т.е. по-прежнему
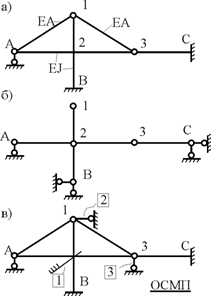
Число неизвестных угловых перемещений nθ остается таким же, как и в случае, когда влиянием продольных сил на конечный результат расчета мы пренебрегаем, т.е. оно равно количеству жестких узлов сооружения. В рассматриваемом случае иным становится число неизвестных линейных перемещений узлов системы nΔ, которое определяется по шарнирной схеме сооружения, образуемой теперь не только введением режущих цилиндрических шарниров в жесткие узлы, но и удалением тех элементов, где требуется учесть продольные силы. Пример 19.9.1. Определить степень кинематической неопределимости рамы, изображенной на рис. 19.27,а с учетом влияния продольных сил во всех стержнях и для ее расчета выбрать основную систему метода перемещений. Шарнирную схему рамы образуем введением во все жесткие узлы, включая и опорные, цилиндрических шарниров и удалением стержней 1А, 12, 2В (рис. 19.27,б). Степень свободы этой шарнирной схемы определим по формуле (19.2): W = 2Y − C − Co = 2 ∙ 4 − 0 − 4 = 4.
Рис. 19.27
Степень кинематической неопределимости рамы равна
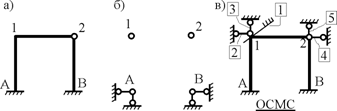
Основная система метода перемещений показана на рис. 19.27,в. Пример 19.9.2. Определить степень кинематической неопределимости комбинированной системы с учетом влияния продольных сил в стержнях 1А и 13 (рис. 19.28,а) и выбрать основную систему метода перемещений для ее расчета.
Рис. 19.28 Шарнирная схема заданной стержневой системы показана на рис. 19.28,б. Обращаем внимание, что при образовании этой шарнирной схемы стержни 1А и 13 удалены. Степень свободы шарнирной схемы  W = 2Y − C − Co = 2 ∙ 6 − 5 − 5 = 2. Степень кинематической неопределимости рамы
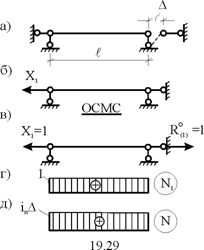
Основная система метода перемещений изображена на рис. 19.28,в. Чаще всего продольные силы при расчетах сооружений учитываются в незагруженных элементах, имеющих на концах цилиндрические шарниры. Продольную силу в таких элементах от взаимного смещения их концов в направлении оси на величину, равную Δ определим методом сил (рис. 19.29,а).
Рис. 19.29
Основная система метода сил показана на рис. 19.29,б. Реакцию в удаленной связи определим из условия
Используя эпюру продольных сил от X1=1 (рис. 19.29,в,г), получим при ЕА=const:
Решив уравнение (19.25), имеем:
где Окончательную эпюру продольных сил определим с помощью соотношения N = N1 X1 (рис. 19.29,д).
Вопросы для самопроверки 1. Сформулируйте допущения, принимаемые при расчете балочных и рамных статически неопределимых систем методом перемещений. 2. Какие величины принимаются за неизвестные в расчетах стержневых систем методом перемещений? 3. Поясните смысл терминов «узел» системы и «элемент» системы. Определите число узлов и элементов в стержневой системе, заданной преподавателем. 4. Каким образом определяется число неизвестных угловых перемещений узлов сооружения? Линейных перемещений узлов сооружения? 5. Как определяется степень кинематической неопределимости сооружения? 6. Как образуется основная система метода перемещений? 7. Какие требования предъявляются к наложению на узлы сооружения линейных связей при образовании основной системы метода перемещений? 8. Задана дважды кинематически неопределимая рамная система, испытывающая силовое воздействие. Требуется: а) выбрать для нее основную систему метода перемещений; б) для ее расчета записать в общем виде систему канонических уравнений метода перемещений; в) пояснить физический смысл каждой строки записанной системы уравнений; г) пояснить смысл величин r11, r12, r21, r22, R1F, R2F, Z1, Z2, r11Z1, r12Z2, r21Z1, r22Z2, входящих в систему уравнений. 9. На базе каких данных производится построение эпюр изгибающих моментов в основной системе метода перемещений от единичных кинематических воздействий и от заданной нагрузки? 10. Перечислите типы стандартных задач, используемых при расчете стержневых систем методом перемещений. Каким образом они могут быть решены от различного вида кинематических и силовых воздействий? 11. Какие способы существуют для вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений? В чем заключается суть статического способа для их определения? Запишите в общем виде выражение для вычисления коэффициентов rii, rij, RiF кинематическим способом. 12. Каким образом можно проверить правильность вычисления коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений? 13. Как производится построение окончательных эпюр внутренних усилий в заданном сооружении при силовом воздействии на него? 14. Сформулируйте смысл статической проверки правильности расчета заданной статически неопределимой системы методом перемещений. 15. В какой-то статически неопределимой раме от заданного силового воздействия методом перемещений получена эпюра изгибающих моментов. Как произвести кинематическую проверку ее достоверности? 16. Задана конкретная комбинированная система, содержащая незагруженные элементы, ограниченные по концам цилиндрическими шарнирами. Определите степень кинематической неопределимости этой системы с учетом влияния продольных сил упомянутых элементов и осуществите выбор соответствующей основной системы метода перемещений.
Рекомендуемая литература 1. Леонтьев Н.Н. Основы строительной механики стержневых систем: Учеб. для вузов / Н.Н. Леонтьев, Д.Н. Соболев, А.А. Амосов. – М.: Изд-во ассоциации строительных вузов, 1996. – 541 с. Глава 7. Расчет рам методом перемещений. § 7.1. Степень кинематической неопределимости системы. § 7.2. Идея метода перемещений. § 7.3. Таблица для определения коэффициентов канонических уравнений. § 7.4. Канонические уравнения метода перемещений и способы вычисления их коэффициентов и свободных членов. § 7.5. Примеры расчета рамы и неразрезной балки на действие нагрузки. – С. 161 – 186. 2. Дарков А.В. Строительная механика: Учеб. для вузов / А.В. Дарков, Н.Н. Шапошников. – М.: Высшая школа, 1986. – 607 с. Глава 7. Расчет статически неопределимых систем методами перемещений и смешанным. § 7.1. Выбор неизвестных в методе перемещений. § 7.2. Определение числа неизвестных. § 7.3. Основная система. § 7.4. Канонические уравнения. § 7.5. Статический способ определения коэффициентов и свободных членов системы канонических уравнений. § 7.6. Определение коэффициентов и свободных членов системы канонических уравнений перемножением эпюр. § 7.7. Проверка коэффициентов и свободных членов системы канонических уравнений метода перемещений. § 7.8. Построение эпюр M, Q и N в заданной системе. – С. 265–288. § 7.11. Пример расчета рамы методом перемещений. – С. 295–302. 3. Смирнов А.Ф. Строительная механика. Стержневые системы: Учеб. для вузов / А.Ф. Смирнов, А.В. Александров, Б.Я. Лащеников, Н.Н. Шапошников. – М.: Стройиздат, 1981. – 512 с. Глава XII. Метод перемещений. § 67. Сущность метода. § 68. Таблица реакций и внутренних усилий в стержне как элементе стержневой системы. § 69. Степень кинематической неопределимости системы. § 70. Канонические уравнения и общий порядок расчета. § 71. Применение теорем о взаимности. – С. 391–420. § 73. Особенности расчета рам с наклонными элементами. – С. 425–430. § 77. Особенности применения метода перемещений с учетом продольных деформаций стержней. – С. 448–450. 4. Клейн Г.К. Руководство к практическим занятиям по курсу строительной механики. Статика стержневых систем: Учеб. пособие / Г.К. Клейн, Н.Н. Леонтьев. – М.: Высшая школа, 1980. – 384 с. Глава XIII. Расчет рам и неразрезных балок методом перемещений. § XIII.1. Последовательность расчета рам. – С. 241–258. § XIII.5. Расчет неразрезных балок. – С. 272–273. 5. Анохин Н.Н. Строительная механика в примерах и задачах. Ч. 2. Статически неопределимые системы: Учеб. пособие / Н.Н. Анохин. – М.: Изд-во ассоциации строительных вузов, 2000. – 464 с. Глава 6. Расчет сооружений методом перемещений. § 6.1. Силовое воздействие. Примеры 6.1–6.7 . – С. 81–101. Примеры 6.9–6.10. – С. 107–111. 6. Проценко В.М. Расчет статически неопределимых рам: Методические указания / В.М. Проценко, В.Г. Себешев. – Новосибирск: НГАС, 1993. – 56 с. Задача № 2. Расчет статически неопределимой рамы методом перемещений. – С. 29–41.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 329. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
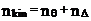 .
.
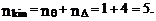
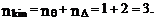
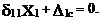 (19.25)
(19.25)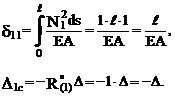
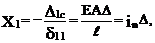 ,
,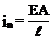 – погонная жесткость стержня при его продольных деформациях.
– погонная жесткость стержня при его продольных деформациях.