
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Система канонических уравнений метода перемещенийПлоская стержневая система с известной топологией и геометрическими размерами испытывает произвольное силовое воздействие (рис. 19.8,а). Изгибную жесткость поперечного сечения стержней, расположенных между узлами сооружения, будем считать постоянной (EJk = const). Задача состоит в определении угловых и линейных перемещений узлов системы от заданной нагрузки (см. п. 19.1 настоящей лекции).
Рис. 19.8
Степень кинематической неопределимости сооружения равна n. Накладывая на его узлы n угловых и линейных связей, образуем основную систему метода перемещений (рис. 19.8,б). Неизвестные угловые и линейные перемещения узлов Z1, Z2,…, Zi,…, Zj,…, Zn определим из условия эквивалентности напряженно-деформированных состояний заданного сооружения (рис. 19.8,а) и его основной системы метода перемещений (рис. 19.8,б), т.е. из условий равенства нулю реакций в наложенных связях от их смещения на величины Z1, Z2,…, Zi,…, Zj,…, Zn и от действующей нагрузки. Другими словами, подбор перемещений угловых и линейных связей в основной системе метода перемещений мы осуществляем, отрицая реакции в наложенных связях, ибо в заданном сооружении этих связей нет. R1 = 0, R2 = 0,…, Ri = 0,…, Rj = 0,…, Rn = 0. (19.3) Используя принцип независимости действия сил, реакции соотношения (19.3) представим в виде суммы реакций от смещений каждой из наложенных связей на величину, совпадающую с величиной соответствующего перемещения узла в заданном сооружении, и от приложенной нагрузки:
………………………………………………………………... (19.4)
………………………………………………………………...
В соотношениях (19.4): 
……………..
……………..
……………..
Из формул (19.5) следует смысл коэффициентов rii и rij. Это реакции в i-й наложенной связи, соответственно от смещения i-й и j-й наложенных связей на величину, равную единице, в основной системе метода перемещений. Подставляя выражения (19.5) в соотношения (19.4), в общем виде получим систему канонических уравнений метода перемещений:
В системе уравнений (19.6) коэффициенты при неизвестных rii, расположенные на главной диагонали, называются главными, коэффициенты rij – побочными, свободные члены RiF – грузовыми коэффициентами. В п. 16.3 шестнадцатой лекции (см. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 3. Статически неопределимые системы. Метод сил: Курс лекций / А.А. Крамаренко, Л.А. Широких. – Новосибирск: НГАСУ, 2002) было показано, что побочные коэффициенты rij и rji подчиняются теореме о взаимности реакций, т.е. rij = rji. Решению системы уравнений (19.6) предшествует определение коэффициентов при неизвестных rii, rij и свободных членов RiF. В методе перемещений перечисленные коэффициенты можно определить, имея эпюры внутренних усилий в основной системе от смещения наложенных связей на величины, равные единице, и от различных видов нагрузок, т.е. имея результаты расчета стандартных стержней на упомянутые воздействия (см. п. 19.2 настоящей лекции). |
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 366. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

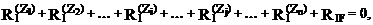
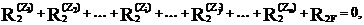

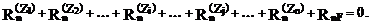
 и
и  соответственно реакции в i-й наложенной связи в основной системе метода перемещений от заданной нагрузки и смещения j-й связи на величину, равную Zj. В соответствии с принципом пропорциональности реакции в наложенных связях запишем так:
соответственно реакции в i-й наложенной связи в основной системе метода перемещений от заданной нагрузки и смещения j-й связи на величину, равную Zj. В соответствии с принципом пропорциональности реакции в наложенных связях запишем так:

 (19.5)
(19.5)

 (19.6)
(19.6)