Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пример расчета рамы на силовое воздействие методом перемещенийПостроить эпюры внутренних усилий от силового воздействия в раме, показанной на рис. 19.16,а. Соотношение между значениями изгибных жесткостей поперечных сечений ригеля (горизонтального элемента) и наклонных элементов задано: EJP : EJH = = 3 : 1,125.
Рис. 19.16 1. Расчет статически определимой части ригеля (рис. 19.16,б – правая консоль) и замена удаленной части соответствующими силами (рис. 19.16,в). 2. Вычисление погонных жесткостей элементов рамы. Сохраняя заданное соотношение между относительными значениями изгибных жесткостей поперечных сечений, примем EJP = 12, EJH = 5. В этом случае имеем (рис. 19.16,в):
3. Определение степени кинематической неопределимости рамы. Число неизвестных угловых перемещений узлов рамы nθ = = 1, так как заданная стержневая система имеет только один жесткий узел, угол поворота которого Z1 от заданного силового воздействия нам неизвестен.
W = 2Y – C – Co = 2 ∙ 3 − 2 −3 = 1. Число независимых линейных перемещений узлов рамы совпадает со степенью свободы ее шарнирной схемы, т.е. nΔ = 1. Степень кинематической неопределимости рамы вычислим по формуле (19.1)
4. Выбор основной системы метода перемещений. Угловую связь («плавающую» заделку) накладываем на узел b, линейную − горизонтально на узел а (рис. 19.16,г). Наложение горизонтальной линейной связи на узел а шарнирной схемы преобразует ее в геометрически неизменяемую систему. Таким образом, за неизвестные метода перемещений в данной задаче приняты угол поворота узла b − Z1 и горизонтальное перемещение узла а − Z2 заданной рамы от действующей на нее нагрузки. Численное значение этих неизвестных определим из системы канонических уравнений метода перемещений (см. п. 19.3 настоящей лекции) 
5. Построение деформационных схем элементов рамы в основной системе метода перемещений от смещения наложенных связей на величину, равную единице (рис. 19.18,а − от поворота угловой связи по часовой стрелке, рис. 19.19,а − от смещения линейной связи по горизонтали влево). Для определения линейных смещений узлов от перемещения горизонтальной наложенной связи влево на величину, равную единице, использован полярный план перемещений (рис. 19.19,б). На рис. 19.19,а показано линейное перемещение всех узлов и, в частности, узла b, который получил линейное перемещение вместе с наложенной на него угловой связью, т.е. не повернувшись.
Рис. 19.18
Рис. 19.19
План перемещений позволяет легко определить перекосы элементов Δ, т.е. относительные отношения их концов в направлениях, перпендикулярных осям элементов в недеформированном состоянии. Из рис. 19.19,б видно, что Dab = 0,75, Dbe = 1,5, DbB = Dec = 1,25. Деформационные схемы, изображенные на рис. 19.18,а и рис. 19.19,а наглядно показывают растянутые и сжатые участки крайних волокон элементов, что позволит в дальнейшем правильно осуществить привязку имеющихся стандартных задач при построении эпюр изгибающих моментов в основной системе метода перемещений. 6. Построение эпюр изгибающих моментов М1 и М2 в единичных состояниях основной системы метода перемещений (рис. 19.18,б и рис. 19.19,в). При построении этих эпюр использованы стандартные задачи, рассмотренные в п. 19.4 настоящей лекции (см. рис. 19.9 и рис. 19.10). Ординаты эпюр изгибающих моментов отложены со стороны вытянутых волокон в соответствии с деформационными схемами, представленными на рис. 19.18,а и 19.19,а. 7. Построение эпюры изгибающих моментов МF в основной системе метода перемещений от заданной нагрузки (рис. 19.20,а, б). Эта операция состоит, по существу, в привязке имеющихся эпюр изгибающих моментов для стандартных стержней различных типов к соответствующим стержням основной системы (см. рис. 19.11 и рис. 19.13).
Рис. 19.20
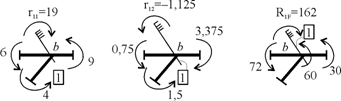
8. Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений (19.22), т.е. реакций r11, r12, r21, r22 в наложенных связях 1 и 2 от единичных кинематических воздействий и реакций R1F и R2F в этих же связях от заданной нагрузки в основной системе метода перемещений статическим способом. Перечисленные реакции изображены на соответствующих деформационных схемах (см. рис. 19.18,а; рис. 19.19,а; рис. 19.20,а). Рассмотрев равновесие узла b в единичных и грузовых состояниях основной системы, получим (рис. 19.21): r11 = 19, r12 = –1,125, R1F = 162.
Рис. 19.21
Рис. 19.22 Реакция в наложенной связи считается положительной, если ее направление совпадает с направлением смещения связи при построении соответствующей деформационной схемы в основной системе метода перемещений, и отрицательной − если не совпадает. В соответствии с теоремой о взаимности реакций имеем: r21 = r12 = –1,125.
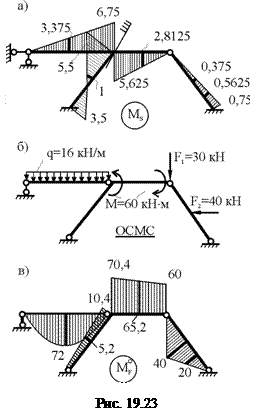
Аналогично вычисляется и реакция R2F для грузового состояния основной системы (рис. 19.22,в) R2F = –Nab = –23,75. Знак «минус» показывает, что направление реакции R2F (направо) противоположно направлению смещения линейной связи 2 (налево). 9. Проверка правильности вычислений коэффициентов при неизвестных и свободных членов системы канонических уравнений (19.22). С этой целью используем суммарную эпюру изгибающих моментов MS = M1 + M2 (рис. 19.23,а). Из основной системы метода перемещений образуем статически определимую основную систему метода сил, удалив все лишние связи, в том числе и наложенные (рис. 19.23,б), и построим в ней грузовую эпюру изгибающих моментов
Суммы реакций соотношений (19.23) и (19.24) известны: r11 + r12 + r21 + r22 = 19 − 2 ∙ 1,125 + 2,2969 = 19,0469, R1F + R2F = 162 − 23,75 = 138,25. Эти же суммы реакций вычислим сопряжением соответствующих эпюр изгибающих моментов
Полезно иметь в виду, что достоверность вычисления побочного коэффициента r12 можно подтвердить, определив статическим способом равный ему побочный коэффициент r21 (рис. 19.22,а), а главных коэффициентов r11 и r22 − сопряжением соответствующих эпюр изгибающих моментов (рис. 19.18,б и рис. 19.19,в)
Эти проверки читателям предлагается выполнить самостоятельно. 10. Решение системы канонических уравнений (19.22).
Z1 = –8,15; Z2 = 6,35. Полученные численные значения Z1 − угла поворота узла b против часовой стрелки (на это указывает знак «минус») и Z2 − горизонтального перемещения узла а влево в рассчитываемой раме от заданной нагрузки являются относительными, так как они вычислены при условно принятых жесткостях поперечных сечений элементов рамы (EJP = 12, EJH = 5). 11. Построение эпюр внутренних усилий в заданной раме. Ординаты эпюры изгибающих моментов в сечениях рамы вычислим, используя соотношение
M = –8,15M1 + 6,35M2 + MF (рис. 19.24,а).
По эпюре изгибающих моментов построим эпюру поперечных сил Q (рис. 19.24,б), а по эпюре Q − эпюру продольных сил N (рис. 19.24,в). Напоминаем читателям, что методика построения эпюр Q и N по имеющейся эпюре изгибающих моментов подробно изложена в п. 5.4 первой части и в п. 8.5 второй части настоящего курса лекций.
Рис. 19.24
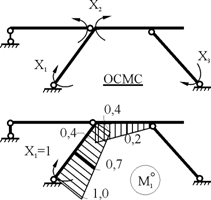
12. Кинематическая и статическая проверки расчета рамы. Используем основную систему метода сил и эпюру изгибающих моментов от X1 = 1, показанные на рис. 19.25.
Рис. 19.25
Кинематическая проверка выполнена с нулевой абсолютной погрешностью вычислений. Для статической проверки запишем условия равновесия для всей рамы (рис. 19.26):
Рис. 19.26
ΣFx = − 40 + (62,82 − 18,79) ∙ 0,6 + (−5,97 + 22,95) ∙ 0,8 = = −40 + 26,4 + 13,6 = 0; ΣFy = 43,36 − 16 ∙ 6 − 30 + (62,82 + 18,79) ∙ 0,8 + + (5,97 + 22,95) ∙ 0,6 = −82,64 + 65,29 + 17,35 = 0.
Приведенные выше условия равновесия строго выполняются.
Читателям предлагается самостоятельно проверить третье условие равновесия для всей рамы, а именно Σmom(F)В = 0,
где В − точка, совпадающая с левой жесткой заделкой наклонной стойки (рис. 19.16,в).
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 347. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |




 Число независимых линейных перемещений nΔ определим по шарнирной схеме, изображенной на рис. 19.17 (см. п. 19.1 настоящей лекции). Степень свободы шарнирной схемы вычислим, используя соотношение (19.2)
Число независимых линейных перемещений nΔ определим по шарнирной схеме, изображенной на рис. 19.17 (см. п. 19.1 настоящей лекции). Степень свободы шарнирной схемы вычислим, используя соотношение (19.2)
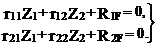 (19.22)
(19.22)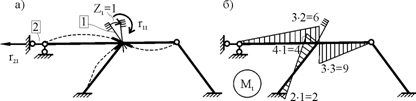



 Из равновесия узла а Σ(Fx)a = 0 следует, что реакция в линейной связи 2 от ее смещения на величину, равную единице (r22), в основной системе метода перемещений равна продольной силе в элементе ab, т.е. r22 = Nab (рис. 19.22,б). Эту продольную силу вычислим, последовательно рассматривая равновесие узлов е и b (Nab = 2,2969). Таким образом, r22 = 2,2969. Читателям предлагается самостоятельно произвести вычисление продольной силы в элементе ab.
Из равновесия узла а Σ(Fx)a = 0 следует, что реакция в линейной связи 2 от ее смещения на величину, равную единице (r22), в основной системе метода перемещений равна продольной силе в элементе ab, т.е. r22 = Nab (рис. 19.22,б). Эту продольную силу вычислим, последовательно рассматривая равновесие узлов е и b (Nab = 2,2969). Таким образом, r22 = 2,2969. Читателям предлагается самостоятельно произвести вычисление продольной силы в элементе ab. (рис. 19.23,в). В соответствии с изложенным в п. 19.6 настоящей лекции имеем:
(рис. 19.23,в). В соответствии с изложенным в п. 19.6 настоящей лекции имеем: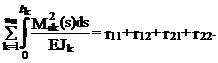 (19.23)
(19.23) (19.24)
(19.24)
 Совпадение левой и правой частей соотношений (19.23) и (19.24) без абсолютных погрешностей свидетельствует о правильности вычисления коэффициентов при неизвестных и свободных членов системы уравнений (19.22).
Совпадение левой и правой частей соотношений (19.23) и (19.24) без абсолютных погрешностей свидетельствует о правильности вычисления коэффициентов при неизвестных и свободных членов системы уравнений (19.22).