
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение коэффициентов при неизвестных и свободных членов системы канонических уравненийКоэффициенты при неизвестных rij и rii и свободные члены RiF системы канонических уравнений метода перемещений (см. п. 19.3 настоящей лекции) можно определить, используя эпюры внутренних усилий, полученные в основной системе от смещения наложенных связей на величину, равную единице, и от заданной нагрузки с помощью стандартных задач (см. п. 19.4 настоящей лекции). Для определения реакций в наложенных связях от вышеупомянутых воздействий используют статический или кинематический способы. Статический способ. Реакция в любой наложенной связи в основной системе метода перемещений от единичных кинематических воздействий и от нагрузки определяется из условия равновесия узла или любой части сооружения, содержащих рассматриваемую связь (см. пример в п. 19.7 настоящей лекции). Кинематический способ. Используя принцип возможных перемещений, определим коэффициенты при неизвестных rij и rii.
Рис. 19.14
Рассмотрим i-е исходное состояние основной системы метода перемещений, в котором i-я наложенная связь получила перемещение на величину, равную единице, и определим реакцию в j-й наложенной связи rji от этого перемещения (рис. 19.14,а). За возможные примем перемещения в j-м состоянии основной системы (рис. 19.14,б). Суммарная возможная работа внешних (Wext,ij) и внутренних (Wint,ij) сил i-го состояния на возможных перемещениях, имеющих место в j-м состоянии, в силу равновесия рассматриваемой системы равна нулю Wext,ij+ Wint,ij = 0. (19.8)
В соотношении (19.8) возможная работа внешних сил запишется: Wext,ij = rji · 1. (19.9) Возможную работу внутренних сил вычислим с учетом только изгибных деформаций (см. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 2. Статически неопределимые системы. Метод сил: Курс лекций / А.А. Крамаренко, Л.А. Широких. – Новосибирск: НГАСУ, 2002. – п.11.2 одиннадцатой лекции) 
После подстановки выражений (19.9) и (19.10) в зависимость (19.8) получим
Если i-е состояние основной системы будем рассматривать как исходное и как вспомогательное, повторно применяя принцип возможных перемещений, вычислим
Для определения реакций в наложенных связях от заданной нагрузки RiF воспользуемся теоремой о взаимности возможных работ состояний F и i, изображенных на рис. 19.15,а,б (см. Крамаренко А.А. Лекции по строительной механике стержневых систем. Ч. 3. Статически неопределимые системы. Метод сил: Курс лекций / А.А. Крамаренко, Л.А. Широких. – Новосибирск: НГАСУ, 2002. – п. 15.1 пятнадцатой лекции).
Так как
то, используя равенство (19.13), получим:
где Перемещение
В соотношении (19.15): Изгибающие моменты
Соотношение (19.15) с учетом зависимости (19.16) перепишется:
После подстановки выражения (19.17) в формулу (19.14) окончательно получим
Вычисление коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений с помощью соотношений (19.11), (19.12) и (19.18), как и в методе сил, можно произвести сопряжением соответствующих эпюр внутренних усилий, используя формулу Симпсона или правило Верещагина. В двадцать второй лекции будет рассмотрено определение коэффициентов при неизвестных и свободных членов системы канонических уравнений метода перемещений в матричной форме.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 354. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |

 (19.10)
(19.10)
 (19.11)
(19.11) (19.12)
(19.12) Из соотношения (19.12) следует, что главные коэффициенты rii системы канонических уравнений всегда положительны. Формула (19.11) по существу подтверждает теорему о взаимности реакций (rji = rij), так как множители Mik(s) и Mjk(s) в подынтегральном выражении можно менять местами.
Из соотношения (19.12) следует, что главные коэффициенты rii системы канонических уравнений всегда положительны. Формула (19.11) по существу подтверждает теорему о взаимности реакций (rji = rij), так как множители Mik(s) и Mjk(s) в подынтегральном выражении можно менять местами.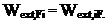 (19.13)
(19.13)

 (19.14)
(19.14) – перемещение в направлении обобщенной силы F от смещения i-й наложенной связи на величину, равную единице в основной системе метода перемещений.
– перемещение в направлении обобщенной силы F от смещения i-й наложенной связи на величину, равную единице в основной системе метода перемещений.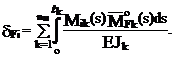 (19.15)
(19.15) – изгибающие моменты в основной системе метода перемещений от смещения i-й наложенной связи на величину, равную единице;
– изгибающие моменты в основной системе метода перемещений от смещения i-й наложенной связи на величину, равную единице;  – изгибающие моменты в любой статически определимой основной системе метода сил, полученной из рассматриваемой основной системы метода перемещений удалением лишних связей, в том числе обязательно и i-й связи, от единичного обобщенного фактора (рис.19.15,в).
– изгибающие моменты в любой статически определимой основной системе метода сил, полученной из рассматриваемой основной системы метода перемещений удалением лишних связей, в том числе обязательно и i-й связи, от единичного обобщенного фактора (рис.19.15,в).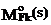 от полного значения обобщенной силы F можно представить в виде
от полного значения обобщенной силы F можно представить в виде отсюда
отсюда (19.16)
(19.16) (19.17)
(19.17) (19.18)
(19.18)