Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема 12Метод наименьших квадратов (МНК)⇐ ПредыдущаяСтр 13 из 13 Понятие о методе наименьших квадратов Пусть имеются результаты серии экспериментов:
где i – номер опыта, xi , yi -результаты эксперимента. Как правило, целью эксперимента является выявление зависимости между величинами x и y. Рассмотрим случай построения оптимальной прямой (полином при m=1) методом наименьших квадратов:y=ax+b. Параметры прямой
Пример выполнения практическойработы 12 Построение оптимальной прямой по методу наименьших квадратов Требуется определить оптимальную прямую для заданных 12 точек на плоскости с координатами
Ручной счет ( Для ручного счета из таблицы координат заданных точек выбираем первые четыре точки. Расчет сведен в табличную форму (см. таблицу ниже):
Подставляем полученные значения в систему уравнений относительно коэффициентов искомой прямой
Решая эту систему, например, по методу Крамера, получим:
Следовательно, Ответ: уравнение искомой прямой имеет вид: Выполнение работы в MATLAB.Для выполнения задания создается М-файл. Исходные данные (массивы x и y) вводятся из файла inpdata.dat. Содержимое указанного файла для рассматриваемого примера имеет вид: 
Ниже приведен текст М-файла. f_id=fopen('inpdata.dat','rt'); x=str2num(fgetl(f_id)); y=str2num(fgetl(f_id)); n=length(x); fprintf('\n Данные эксперимента:') fprintf('\n x:'); fprintf('%5.1f',x); fprintf('\n y:'); fprintf('%5.1f',y); p1=polyfit(x,y,1); a=p1(1); b=p1(2); s=0; for i=1:n s=s+(a*x(i)+b-y(i))^2; end fprintf('\n МНК-прямая: \n y=%8.4f',a); fprintf('*x+%8.4f',b); fprintf(' s=%8.4f \n',s); y1=polyval(p1,x); plot(x,y,'r*',x,y1); title('График оптимальной прямой и экспериментальные точки'); grid on xlabel('x');ylabel('y'); Данные эксперимента: X: 1.0 2.0 3.0 4.0 4.0 5.0 3.0 6.0 10.0 8.0 9.0 7.0 Y: 2.0 2.5 2.0 4.0 4.5 5.0 4.0 5.0 9.0 7.0 8.0 7.0
МНК-прямая y= 0.7918x+ 0.9089 s= 3.2807
Контрольные вопросы к практической работе 12 1. Для своих данных построить оптимальную кривую второго порядка. 2. Отобразить на графике оптимальные прямые для 4 и 12 точек. 3. Для чего используется в программном коде функция polyval? 4. Для чего используется в программном коде функцияpolyfit? 5. Запрограммируйте решение своей задачи через реализацию формул метода наименьших квадратов по формуле 12.1 Тема 13 Задача линейного программирования Формулировка задачи линейного программирования Многие практические задачи, связанные с планированием производства, экономические задачи, расчет конструкций и т.д. сводятся к, так называемой, задаче математического программирования. Такая задача состоит в вычислении максимума (минимума) функции цели Практическая работа 13 посвящена решению задачи линейного программирования. Необходимо найтиточку максимума функции цели при заданных ограничениях Задачу необходимо решить 1. вручную геометрическим методом. 2. на компьютере с помощью системы MATLAB. 1. вручную геометрическим методом в соответствии с примером в теоретической части. 2. на компьютере с помощью системы MATLAB, Excel. Для компьютерного счета Представим задачу в матричной формулировке, т.е. найти
при ограничениях
и дополнительном условии
где Пример выполнения практической работы 13 Ручной счет Для решения воспользуемся геометрическим методом. Для функция цели:
Строим многоугольник ограничений W (допустимую область значений
Из чертежа видно, что среди точек многоугольника ограничений наиболее удаленной точкой от прямой Ответ: Компьютерный счет Программа на MATLAB представлена ниже: %Задание количества неизвестных n=input('Введите n='); %Задание количества ограничений m= input('Введите m='); g= input('введите g='); s= input('введите s='); %Формирование вектора коэффициентов функции цели c=[s;g]; %Формирование матрицы коэффициентов ограничений A=[-1/g -1/s; -s 2*g; 2*s -g]; %Формирование вектора правых частей ограничений b=[-0.25; g*s ; g*s]; %Распечатка исходных данных disp('Вектор коэффициентов функции цели, с'); fprintf('%12.4f \n',c); disp('Матрица коэффициентов ограничений, A'); for k=1:m fprintf('%12.4f',A(k,:)); fprintf('\n') end disp('Вектор правых частей ограничений, b '); fprintf('%12.4f \n',b);
%Задание вектора ограничений снизу на координаты lb= zeros(2,1); %Обращение к функции MATLAB для решения зпадачи %линейного программирования [x,z]=linprog(-c,A,b,[],[],lb);
%Распечатка результатов disp('Вектор решения, x'); fprintf('%12.4f \n',x); fprintf('Максимальное значение функции цели,z=%12.4f',z);
Результаты расчета Введите n= 2 Введите m= 3 введите g= 3 введите s=12 Вектор коэффициентов функции цели, с 12.0000 3.0000 Матрица коэффициентов ограничений, A -0.3333 -0.0833 -12.0000 6.0000 24.0000 -3.0000 Вектор правых частей ограничений, b -0.2500 36.0000 36.0000 Optimization terminated.
Векторрешения, x 3.0000 12.0000 Максимальное значение функции цели,z= -72.
Контрольные вопросы к практической работе 13 1. Задача линейного программирования. Основные понятия. Примеры 2. Геометрическая интерпретация задачи линейного программирования. 3. Решение задачи линейного программирования 4.Найти (если есть) min и max функции
5. Найти (если есть)min и max функции
Оглавление Введение. 2 Тема 1 Простейшие вычисления в MATLAB Арифметические выражения. 3 Тема 2 Логические выражения. Условный оператор. 7 Тема 3. Определение наибольшего и наименьшего значения функции на отрезке и построение ее графика. 12 Тема 4 Вычисление суммы.. 15 Тема 5 Массивы.. 19 Тема 6 Вычисление скалярного произведения векторов. 23 ЧИСЛЕННЫЕ МЕТОДЫ И АЛГОРИТМЫ... 27 Тема 7 Решение задач методом Гаусса. 27 Тема8 Итерационные методы решения системы линейных алгебраических уравнений. 35 Тема 9 Методы вычисление собственных значений и собственных векторов матриц. 42 Тема 10Методы численного интегрирования. 45 Тема 11 Методы решения нелинейных уравнений. 50 Тема 12 Метод наименьших квадратов (МНК) 55 Тема 13 Задача линейного программирования. 58
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 389. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 и
и  определяются из системы уравнений:
определяются из системы уравнений: (12.1)
(12.1)
 .Координаты точек представлены в таблице:
.Координаты точек представлены в таблице: 

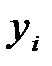
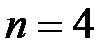 ).
).


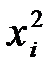
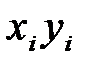

 и
и  :
:
 ,
,  ,где
,где ,
, ,
, 
 ,
,  .
. . График выведен на рисунке.
. График выведен на рисунке. ,
,  при заданных ограничениях
при заданных ограничениях  ,
,  ,
,  . Наиболее простым представителем такой задачи является задача линейного программирования
. Наиболее простым представителем такой задачи является задача линейного программирования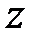 :
: 
 ,
,

 ,
,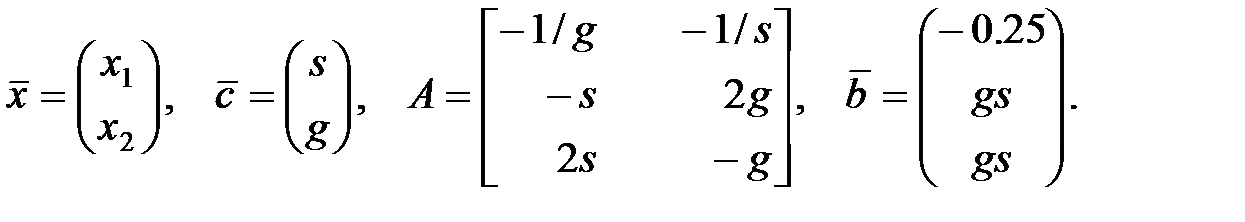
 ,
,  . Тогда условия задачи принимают следующий вид:
. Тогда условия задачи принимают следующий вид: , ограничения:
, ограничения:
 и
и  ) прямую
) прямую  .
.
 является максимальной.
является максимальной. .
. при ограничениях:
при ограничениях:
 при ограничениях:
при ограничениях: