
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Пример выполнения практической работы 6Вычислить скалярное произведение s=(Ap,B(q+r)) при
Алгоритм решения задачи: 1. Вычисляем x=Ap 2. Вычисляем y=q+r 3. Вычисляем z=By 4. Вычисляем s=(x,z) Ручной счет 1. 2. 3. 4. s=(x,z)= Ответ: s=(Ap,B(q+r))=33.17 Найдем скалярное произведение тремя способами.
Третий способ.Запрограммируем вычисления всех операций.
Результатвсех способов: s = 33.1700 Контрольные вопросы к практической работе 6 1. Написать программу, формирующую матрицу А по правилу несколькими способами: 
2. Написать программу, формирующую матрицу А по правилунесколькими способами:
3. Написать программу, формирующую матрицу А по правилунесколькими способами:
4. Пользователь вводит размер формируемой матрицы. Написать программу, формирующую матрицу А по правилунесколькими способами:
5. Какие параметры называются формальными? фактическими? Какая между ними связь?
ЧИСЛЕННЫЕ МЕТОДЫ И АЛГОРИТМЫ Тема 7Решение задач методом Гаусса Основные записи СЛАУ В общем случае основная запись системы n линейных алгебраических уравнений с n неизвестными имеет следующий матричный вид:
где
A –матрица коэффициентов системы; Классификацию СЛАУ можно представить в виде схемы (рис.7.1)
Рис.7.1 Классификация СЛАУ Расширенная матрица- получается из матрицы коэффициентов системы путем добавления к этой матрице столбца свободных членов:
где Общая схема метода Гаусса Решение СЛАУ методом Гауссасостоит из двух частей: · 1-я часть – приведение к эквивалентной системе уравнений более простой структуры (треугольной) за счет вычитания уравнений друг из друга, при умножении вычитаемого уравнения на специально подобранное число (Прямой ход). · 2-я часть – решение равносильной системы уравнений с треугольной матрицей (Обратный ход). Запишем общие формулы прямого хода:
Замечание. Элемент Обратный ход(решение системы с треугольной матрицей): Из треугольной системы последовательно (в обратном порядке) вычисляются значения неизвестных по формуле:
для i=n, n-1, n-2, ..., 2, 1 (при i=n сумма в формуле отсутствует). |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 345. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
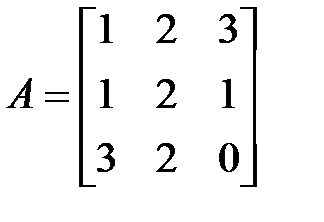 ;
; 
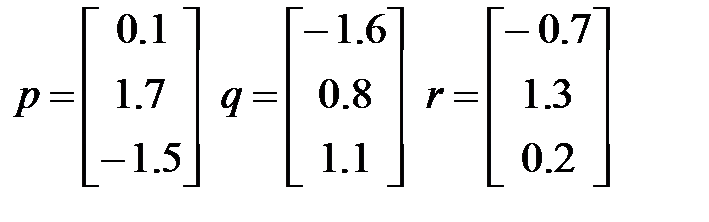

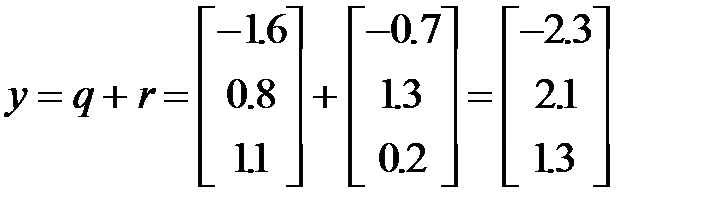 ,
, ,
,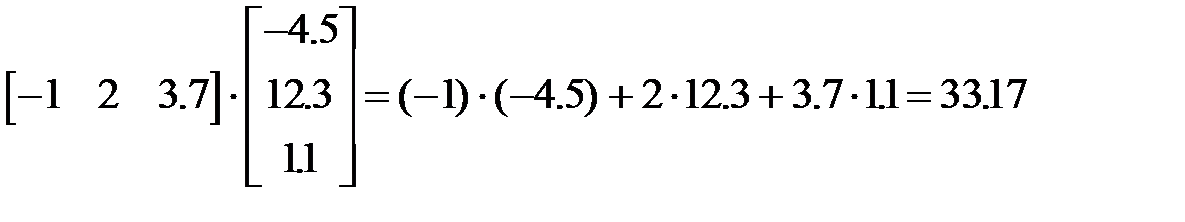
 . Пользователь вводит только размер формируемой матрицы.
. Пользователь вводит только размер формируемой матрицы. . Пользователь вводит только размер формируемой матрицы.
. Пользователь вводит только размер формируемой матрицы. . Пользователь вводит только размер формируемой матрицы.
. Пользователь вводит только размер формируемой матрицы.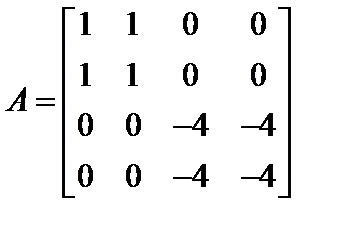 . Необходимо выполнить проверку четности размерности.
. Необходимо выполнить проверку четности размерности. ,
,
 ;
;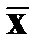 –вектор неизвестных;
–вектор неизвестных; 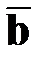 –вектор свободных членов.
–вектор свободных членов.

 .
.
 - называется ведущим элементом.
- называется ведущим элементом.