
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производственная функция Кобба-ДугласаБудем считать, что для рассматриваемой экономической системы определён частный случай производственной функции – производственная функция Кобба-Дугласа, которая имеет вид Y = C K где С – масштабный множитель. Легко показать, что эта функция удовлетворяет всем свойствам неоклассической производственной функции, Рассмотрим основные показатели эффективности производства производственной функции Кобба-Дугласа. Средняя фондоотдача и средняя производительность труда определятся из соотношений AyK = Y/K = C (L/K)1- Предельная фондоотдача и предельная производительность труда определяются из соотношений Мyk = МyL = Из (3.7) и (3.8) следует, что Мyk = С учётом 0 < Эластичность выпуска по капиталу и труду определяется из соотношений Изменение выпуска производимого продукта при одновременном изменении объёмов затрачиваемых факторов определится из соотношения Y(K+  Пример 3.1. Пусть производственная система характеризуется производственной функцией Кобба-Дугласа. За период времени системой было произведено 100 единиц продукции при затратах 20 единиц труда и 40 единиц капитала. Известно, что 1. Записать производственную функцию Кобба-Дугласа. 2. Сколько единиц продукта будет произведено системой при затратах 25 единиц труда и 50 единиц капитала? 3. Определить для данной производственной системы средние продукты труда и капитала 4. Определить предельные продукты труда и капитала. 5. Проверить вычислениями равенства (3.10). Решение 1. Подставим в (3.5) исходные данные: 100 = С*400.75*200.25. После вычислений получим: 100 = С*33,64 или С = 100/33,64 = 2,973. Окончательно имеем: Y = 2,973 K0,75L0,25. 2. Подставим в полученное выражение для производственной функции новые данные: Y = 2,973*500,75*250,25 = 125. Таким образом, системой при новых данных будет произведено 125 единиц продукта. 3. Подсчитаем средние продукты факторов, используя формулы (3.6). AyK = 100/40 = 2,5. И AyK = 2,973* (20/40)0,25 = 2,5; AyL = 100/20 = 5. И AyL = 2,973*(40/20)0,75 = 5. Как видим, проверяемые равенства выполняются точно, если при вычислениях не производить округления. 4. Рассчитаем предельный продукт капитала: МyK = Аналогично предельный продукт труда МyL = (1– Сравнивая средние и предельные продукты факторов, видим, что действительно, предельные продукты меньше средних, подтверждая тем самым закон убывающей эффективности факторов. Средний продукт капитала, равный 2,5, означает, что в рассматриваемой экономической системе на единицу основных фондов приходится в среднем 2,5 единиц выпускаемого продукта, а предельный продукт капитала, равный 1,875, означает, что в экономической системе на единицу прироста основных фондов приходится в среднем 1,875 единиц прироста выпуска продукта. Аналогично и по продукту труда. 5. Пусть левая часть выражения (3.10) – это выпуск, подсчитанный в п. 7.2 при Y +
Функция затрат Анализ затрат в производственных системах играет важную роль в принятии управленческих решений. При выборе оптимального варианта производства продукции нужно сравнивать возможные альтернативы и выбирать решение, которое обеспечивает минимальные затраты при заданном выпуске производимой продукции или максимальный выпуск продукции при заданном уровне используемых ресурсов. Известно, что эти две задачи: максимизации выпуска при фиксированной полной стоимости ресурсов и минимизации полной стоимости ресурсов при фиксированном уровне выпуска – имеют одинаковое решение и называются двойственными. Рассмотрим первую задачу, введя понятие функции затрат производственной системы. Функция затрат равна минимальной полной стоимости набора ресурсов, необходимого для выпуска заданного количества продукта. Пусть производственная система задана производственной функцией
где Задача может быть решена методом множителей Лагранжа, для чего построим функцию Лагранжа и приравняем её частные производные по
Решая эту систему из трёх уравнений с тремя неизвестными Вычислим функцию затрат для частного случая производственной системы, которая описывается производственной функцией Кобба-Дугласа. Пусть задано бюджетное ограничение, которое определяется полной стоимостью набора ресурсов
Это и есть затраты экономической системы, необходимые для производства фиксированного уровня получаемого продукта. Определим величину
Тогда, при заданном
где При изменении величины
Найдём значение величины
Таким образом, точка оптимального выпуска задаётся отношением стоимости капитала к полной стоимости потребляемых ресурсов равным Количество максимально возможного выпуска при этом будет равно (при фиксированных затратах С)
Функцию затрат в этом случае представим как минимальные средние затраты на единицу выпускаемого продукта, разделив
Следует обратить внимание, что функция затрат определяется ценами единицы труда и капитала, которые определяются состоянием рынка ресурсов производства и являются экзогенными величинами, заданными внешней экономической средой. В заключение отметим, что в нашем случае мы выписали функцию затрат лишь для частного случая производственной функции – функции Кобба-Дугласа. Для других производственных функций функции затрат будут другими. Каждой производственной функции соответствует своя функция затрат.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 412. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 L1-
L1-  Y/
Y/  K,L+
K,L+  Y +
Y +  . Кроме того, известны объём платёжных средств производителя С и цены единицы труда
. Кроме того, известны объём платёжных средств производителя С и цены единицы труда  и капитала r. Будем предполагать, что цены единицы труда
и капитала r. Будем предполагать, что цены единицы труда 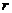 определены рынком ресурсов и являются постоянными величинами. Для нахождения функции затрат необходимо решить задачу оптимизации:
определены рынком ресурсов и являются постоянными величинами. Для нахождения функции затрат необходимо решить задачу оптимизации: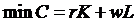 ;
;
 и
и  – положительные постоянные, а K и L необходимо определить.
– положительные постоянные, а K и L необходимо определить. и
и  к нулю:
к нулю: ;
; ;
;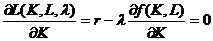 ;
; .
. и ценами единицы труда
и ценами единицы труда  .
. как отношение стоимости капитала к полной стоимости капитала и труда:
как отношение стоимости капитала к полной стоимости капитала и труда: .
.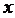 имеем соотношения для затрат капитала и труда:
имеем соотношения для затрат капитала и труда: и
и  ,
, и
и  – это максимальное количество капитала и труда, которое можно приобрести на сумму
– это максимальное количество капитала и труда, которое можно приобрести на сумму 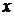 стоимость набора ресурсов остаётся постоянной, а количество получаемого продукта изменяется и может быть определено по формуле
стоимость набора ресурсов остаётся постоянной, а количество получаемого продукта изменяется и может быть определено по формуле .
.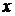 , при котором выпуск продукции достигает максимума. В этой точке производная производственной функции
, при котором выпуск продукции достигает максимума. В этой точке производная производственной функции  обращается в нуль.
обращается в нуль.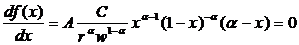 .
. ).
). ,
, 
 :
: .
.