Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Двойственность в линейном программировании
Рассмотрим стандартную и двойственную к ней задачи линейного программирования. Стандартная задача: Найти значения переменных х1, х2, ..., хn, удовлетворяющих условиям Двойственная задача: Найти значения переменных у1, у2, ..., уm, удовлетворяющих условиям Условия (4.1) и (4.5), а также (4.2) и (4.4) называются взаимносопряжёнными. Приведём формулировки основных теорем двойственности, необходимые для дальнейшего рассмотрения.
Теорема 1 (основная). Если задача (4.1) – (4.3) имеет оптимальное решение х*, то и двойственная к ней задача (4.4) – (4.6) также имеет оптимальное решение у*, причём Теорема 2 (о равновесии). Для каждой пары сопряжённых условий в оптимальном решении прямой и двойственных задач выполняются следующие соотношения: если одно из них выполняется как строгое равенство, то другое – как строгое неравенство и наоборот, т.е. если если если  если Примечание: в случае вырожденного решения одной из задач оба взаимносопряжённых условия выполняются как строгие равенства.
4.2 Экономическая интерпретация и свойства двойственныхоценок
Для формулировки свойств двойственных оценок придадим задачам (4.1) – (4.3) и (4.4) – (4.6) конкретный экономический смысл. Прямая задача Пусть в производстве n видов продукции используется m видов ресурсов. Известны величины Двойственная задача Найти уi – оценки единицы каждого вида ресурсов, минимизирующих суммарную оценку ресурсов, при условии, что оценка ресурсов, необходимых для производства единицы каждого вида продукции, была бы не меньше цены единицы соответствующей продукции. уi – оценка i-ro ресурса с точки зрения его лимитированности в оптимальном плане (теневая цена i-ro ресурса). Свойство 1. Оценка как мера влияния ограничения на оптимальное значение целевой функции. Это свойство показывает ещё одну связь между переменными прямой и двойственной задач. Поясним это подробнее. Пусть х* = (х1*, х2*, ..., хj*, ... , хn*) – оптимальное решение прямой задачи, а у* = (у1*, у2*, ..., уi*, ..., уm*) – оптимальное решение двойственной задачи: Zmax = С1x1* + ... + Сjxj* + ... + СnХn*; Wmin = b1y1* + ... + biyi* + ... + bmym*. На основании первой теоремы двойственности (Zmax = Wmin) можно записать С1х1* + ... + Сjxj* + ... + Сnхn* = b1у1* + ... + biуi* + ... + bmym*. Отсюда следует, что Zmax = b1у1* + ... + biуi* + ... + bmym*. Поставим вопрос: как изменится величина Zmax, если в исходной задаче увеличить свободный член b в i-м ограничении-неравенстве на величину Величина Zmax, рассматриваемая теперь как функция переменных b1, b2, ..., bi, ..., bm, получит приращение ∆Zmax. Частные производные этой функции по любому из этих аргументов (при условии неизменности остальных) имеют вид
Учитывая, что функция Zmax линейная, получим ∆Zmax = yi ∙ ∆bi, т.е. при увеличении объёма i-гo ресурса на единицу (∆bi = 1) оптимальное значение целевой функции увеличится на оценку единицы этого ресурса. Если же объём i-гo ресурса изменить на k единиц, то целевая функция изменится на величину k ∙ уi* при условии, что это изменение не выйдет за границы устойчивости двойственных оценок. Свойство 2.Оценка как мера дефицитности ресурса. Это свойство следует из теоремы 2. Если уi* = 0, то из (4.9) следует, что Свойство 3. Оценка как мера эффективности выпускаемой продукции. Это свойство также следует из теоремы 2. Пусть хj* > 0. Это означает, что продукция вида j производится в оптимальном плане. Из (4.11) имеем Свойство 4. Оценка как средство балансировки затрат и результатов в оптимальном плане. Это свойство следует из условия (4.7) теоремы 1:
Левая часть этого равенства означает стоимость произведённой продукции, т.е. результат производства, а правая – оценку используемых ресурсов, т.е. затраты экономической системы. Следовательно, в оптимальном плане результаты производства балансируются затратами системы на это производство. В случае неоптимальности плана по известной теореме линейного программирования
т.е. для произвольного плана задачи результат не больше затрат на производство.
4.3 Анализ чувствительности модели
В большинстве случаев принятия решений полезно составить предварительный план действий, чтобы проанализировать, какое воздействие на принятое решение окажут изменения, вносимые в исходную задачу. Большое значение в линейном программировании имеет анализ чувствительности модели. Этот метод позволяет учесть: – воздействие дополнительного количества лимитирующего ресурса; – воздействие дополнительного количества нелимитирующего ресурса; – воздействие изменений в коэффициентах целевой функции. Итоговая симплексная таблица при решении задачи линейного программирования содержит оптимальное значение целевой функции, значения основных и балансовых переменных. Последние, как известно, соответствуют остаткам ресурсов. Кроме того, в ней указываются оценки (теневые цены) ресурсов. Информацию итоговой таблицы симплексного метода можно использовать также в анализе чувствительности модели, чтобы выявить общее воздействие изменений в запасах лимитирующих ресурсов и в коэффициентах целевой функции на значение целевой функции. При определении интервалов изменения коэффициентов целевой функции необходимо вычислить пределы увеличения и уменьшения этих коэффициентов по формулам
где yi* – двойственные оценки в оптимальном решении (элементы Z – строки итоговой симплексной таблицы); dpi – элементы строки, соответствующей р-й базисной переменной в итоговой симплексной таблице. Интервал изменения коэффициента Ср при переменной хр в целевой функции имеет вид Если изменение коэффициента Ср находится в интервале (4.12), то состав базисных переменных и их значения в оптимальном плане не изменятся. Если же изменение Ср не входит в интервал изменения (4.12), то в оптимальном плане изменятся и состав базисных переменных и их значения. В случае если переменная хk не входит в базис оптимального решения, то интервал изменения коэффициента Сk будет [0; Сk + уk* ], где уk* – оценка балансовой переменной хk в оптимальном плане (находится в Z-строке), показывающая превышение оценки затрат ресурсов над ценой единицы k-й продукции. Аналогично находятся границы изменения правых частей ограничений где Здесь xj* – значения базисных переменных в оптимальном решении исходной задачи. Если изменения правых частей ограничений не выйдут за пределы интервала (4.13), то структура базисных переменных окажется той же, что и в оптимальном решении, а их значения изменятся. При этом оценки оптимального плана (значения yi* в Z-строке) не изменятся и их можно использовать для оценки изменённой целевой функции.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 336. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ; (4.1)
; (4.1) ; (4.2)
; (4.2) . (4.3)
. (4.3) ; (4.4)
; (4.4)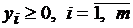 ; (4.5)
; (4.5) . (4.6)
. (4.6) . (4.7)
. (4.7) то
то 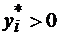 ; (4.8)
; (4.8) то
то 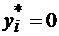 ; (4.9)
; (4.9) то
то  ; (4.10)
; (4.10) то
то  (4.11)
(4.11) , характеризующие нормы расхода каждого вида ресурса на производство единицы каждого вида продукции
, характеризующие нормы расхода каждого вида ресурса на производство единицы каждого вида продукции  . Найти хj – план производства каждого вида продукции, при котором расходы ресурсов не превышали бы имеющихся запасов (bi), a общий доход (Z) от реализации произведённой продукции был бы максимальным.
. Найти хj – план производства каждого вида продукции, при котором расходы ресурсов не превышали бы имеющихся запасов (bi), a общий доход (Z) от реализации произведённой продукции был бы максимальным. .
.
 т.е. i-й ресурс не полностью используется в оптимальном плане и его оценка равна нулю. В соответствии с 1-м свойством, увеличение объёма этого ресурса не приведёт к увеличению объёма выпускаемой продукции. Такой ресурс будем называть недефицитным (нелимитирующим). Для недефицитного ресурса значение соответствующей балансовой переменной показывает его остаток после выполнения оптимального плана. Если уi* > 0, то из (4.8) имеем
т.е. i-й ресурс не полностью используется в оптимальном плане и его оценка равна нулю. В соответствии с 1-м свойством, увеличение объёма этого ресурса не приведёт к увеличению объёма выпускаемой продукции. Такой ресурс будем называть недефицитным (нелимитирующим). Для недефицитного ресурса значение соответствующей балансовой переменной показывает его остаток после выполнения оптимального плана. Если уi* > 0, то из (4.8) имеем  т.е. если i-й ресурс полностью расходуется в оптимальном плане, то его оценка положительна. Такой ресурс будем называть дефицитным (лимитирующим). Чем больше оценка ресурса, тем он дефицитнее с точки зрения его вклада в результат производства. Величина, на которую увеличивается значение целевой функции при увеличении количества лимитирующего ресурса на единицу, называется оценкой ресурса или его теневой ценой. Теневая цена ресурса – это оценка единицы данного ресурса в оптимальном решении.
т.е. если i-й ресурс полностью расходуется в оптимальном плане, то его оценка положительна. Такой ресурс будем называть дефицитным (лимитирующим). Чем больше оценка ресурса, тем он дефицитнее с точки зрения его вклада в результат производства. Величина, на которую увеличивается значение целевой функции при увеличении количества лимитирующего ресурса на единицу, называется оценкой ресурса или его теневой ценой. Теневая цена ресурса – это оценка единицы данного ресурса в оптимальном решении. т.е. оценка ресурсов на производство единицы j-й продукции равна стоимости единицы этой продукции. Такую продукцию будем считать рентабельной. Если хi* = 0, то из (4.10) следует, что
т.е. оценка ресурсов на производство единицы j-й продукции равна стоимости единицы этой продукции. Такую продукцию будем считать рентабельной. Если хi* = 0, то из (4.10) следует, что 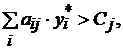 т.е. продукция j-го вида в оптимальном плане не производится, потому что аналогичная оценка ресурсов превышает цену единицы этой продукции. Такую продукцию будем считать нерентабельной.
т.е. продукция j-го вида в оптимальном плане не производится, потому что аналогичная оценка ресурсов превышает цену единицы этой продукции. Такую продукцию будем считать нерентабельной.

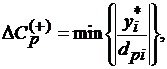
 для dpi < 0;
для dpi < 0; для dpi > 0,
для dpi > 0, . (4.12)
. (4.12)  (4.13)
(4.13)