Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Исследование и решение системы уравнений модели межотраслевого балансаТаблица МОБ позволяет изучать структуру потоков ресурсов, однако для понимания функционирования экономики, в частности эффекта распространения (мультипликации), необходимо сделать ещё один шаг, заключающийся в построении коэффициентов прямых затрат и коэффициентов полных затрат. Будем, следуя автору модели, американскому учёному русского происхождения В. Леонтьеву, считать, что объёмы промежуточного производственного потребления прямо пропорциональны объёмам производства продукции потребляющих отраслей: xij = aij xj (i,j = где коэффициентами пропорциональности aij являются коэффициенты прямых материальных затрат, определяемые из соотношений: aij = xij / xj (i,j = Из (2.5) следует и смысл этих коэффициентов; они показывают объём материальных ресурсов i-го вида, необходимый для производства единицы валового продукта j-го вида. После подстановки (2.4) в (2.1) получаем Это и есть система уравнений модели В. Леонтьева “затраты – выпуск”, называемая статической моделью МОБ. Статической она является потому, что отражает производство и основные потоки продукции между отраслями за фиксированный промежуток времени (обычно за год), в течение которого все параметры модели остаются постоянными. Получив систему уравнений (2.6), мы вплотную подошли к центральному вопросу межотраслевого анализа: как изменится объём валового выпуска i-й отрасли (xi), если при фиксированных коэффициентах прямых затрат aij значение yi изменится на величину Dyi. Отметим, что соотношение (2.4) предполагает существование производственной функции с неизменным эффектом масштаба (затраты прямо пропорциональны выпуску) и с отсутствием взаимозаменяемости ресурсов (соотношение затрат ресурсов фиксировано и не зависит от уровня выпуска). Кроме того, здесь учитываются только затраты промежуточных продуктов, затраты факторов производства опущены. Для ответа на поставленный вопрос необходимо найти решение xi (i =  Запишем систему уравнений (2.6) в матричной форме: X = AX + Y , (2.7)
(2.7) является леонтьевской моделью МОБ. Решим это уравнение относительно Х, определив валовой выпуск отраслей, обеспечивающий заданный уровень спроса Y на конечную продукцию отраслей: X – AX = Y, (E – A) X = Y, X = (E – A)-1 Y. (2.8) Последняя формула, как известно, может быть записана, если существует обратная матрица к матрице (Е – А). Рассмотрим кратко вопрос о существовании и свойствах матрицы В = (Е – А)-1. Матрица А коэффициентов прямых материальных затрат в случае стоимостного межотраслевого баланса относится к хорошо изученному в математике классу матриц. В силу экономического смысла все диагональные элементы матрицы А должны быть меньше единицы (aii < 1, Доказано, что перечисленные выше условия для элементов матрицы А являются необходимыми и достаточными, чтобы матрица А и соответствующая ей экономика были продуктивными, т.е. чтобы существовали неотрицательные векторы X ³ 0 и Y ³ 0, такие, что X – AX = Y. Из продуктивности матрицы А следует, что существует обратная матрица (Е – А)-1 и все её элементы неотрицательны, а также имеет место разложение: (Е – А)-1 = Е + А + А2+…..+ Аm +…., (2.9) причём Am ® 0, при n ®¥. Стремление матрицы Am к нулевой настолько быстрое, что уже первых несколько членов этого разложения достаточно для вычисления обратной матрицы с большой точностью. Заметим, что формула (2.9) часто используется для вычисления обратной матрицы большой размерности. Матрица В = (Е – А) –1 (2.10) называется обратной матрицей Леонтьева, или матричным мультипликатором, или мультипликатором Леонтьева. Выясним её экономический смысл, для чего (2.8) распишем подробнее (с учётом обозначения (2.10)) X = B Y или откуда Подставим (2.9) в (2.11) и получим: X = (E – A)-1 Y = (E + A + A2 + …+ Am + …) Y, откуда X = Y + AY + A2Y +…+ AmY + … . Итак, валовой выпуск, обеспечивающий производство конечного спроса в объёме Y, состоит из самого конечного спроса Y плюс величины AY, являющейся результатом первичного эффекта распространения, плюс A2Y – вторичного и т.д. Элементы матрицы В называются коэффициентами полных материальных затрат. С учётом линейности соотношений (2.11) эффект распространения DX, вызванный изменением конечного спроса на величину DY рассчитывается как DX = B DY. Кроме того, говорят, что решение системы уравнений МОБ позволяет определить равновесный выпуск, имея в виду под общим равновесием такое соотношение экономической системы, которое характеризуется равновесием спроса и предложения всех ресурсов. Как мы видели, равновесный выпуск определяется из системы уравнений распределения продукции (2.1). Система уравнений производства продукции является основой для получения равновесных цен. Равновесные цены позволяют исследовать ценовой аспект эффекта распространения и построить ценовую модель МОБ. Обозначим vj = zj / xj – величину добавленной стоимости, приходящейся на единицу валовой продукции отрасли и называемой долей добавленной стоимости. Тогда, учитывая, что zj = vj xj , (2.2) перепишем в виде: или Это выражение описывает формирование цен каждого вида продукции в базовом периоде, если их принять за единицу. Слагаемое Если для расчётного периода доля добавленной стоимости будет равна vj, то цены P(j = В матричном виде эту систему можно переписать как Р = Ат Р + V , (2.14) где Матрица Ат – транспонированная матрица А. Решим (2.14) относительно Р. Получим P – AT P = V ; (E –AT) P = V ; P = (E – AT)-1 V ; P = [(E – AT)-1 ] T V или P = BT V (2.15) Уравнения (2.13) и (2.14) называют моделью равновесных цен, а матрицу Вт – ценовым матричным мультипликатором (матричным мультипликатором ценового эффекта распространения). Эффект распространения DР, вызванный изменением доли добавленной стоимости на DV, может быть рассчитан из (2.15) как DP = BT DV. 2.3 Балансы трудовых ресурсов и основных производственных фондов
Все виды затрат в конечном счёте сводятся к затратам труда, труд является единственным источником стоимости, поэтому трудовые показатели МОБ играют важную роль в решении проблемы измерения затрат и результатов национального производства, его эффективности. Упрощённый межотраслевой баланс труда описывается уравнением L где tj – коэффициенты прямых затрат труда в j-й отрасли; tj = Lj / xj (Lj – объёмы затрат труда в j-й отрасли). Учёт трудовых ресурсов предполагает наравне с решением системы уравнений по производству и распределению продукции рассматривать также баланс трудовых ресурсов. Кроме того, дополним схему МОБ производства и распределения продукции балансом основных фондов где fj – коэффициенты прямой фондоёмкости в j-й отрасли; fj = Фj / xj (Фj – наличие фондов в j-й отрасли). Баланс основных фондов может, в частности, ограничивать объёмы выпуска продукции, вместе с тем вектор конечного продукта, включая в себя фонд производственного накопления, является ограничением на возможный прирост основных фондов, поэтому учёт этого баланса также важен в решении задачи определения сбалансированного выпуска. В матричной записи (2.16) и (2.17) примут вид L = t Х , Ф = f Х . Перепишем их с учётом (2.11), получим L = t Х = t B Y = t Y ; (2.18) Ф = f Х = f B Y = j Y , (2.19) где t = t B или tk j = f B или j k Коэффициенты tk и j k называются соответственно коэффициентами полных затрат труда и фондов и показывают, как это следует из (2.20) и (2.21), потребность в соответствующих ресурсах во всех отраслях национальной экономики для производства единицы конечного продукта в k-й отрасли. А (2.18) и (2.19) показывают, что прямые затраты ресурса на выпуск валовой продукции совпадают с их полными затратами на выпуск конечного продукта. Уменьшение полных затрат труда на единицу продукции является обобщающим показателем роста производительности труда, эффективности общественного производства. Аналогично и для затрат основных фондов. Поэтому коэффициенты полных затрат труда и фондов являются ценным инструментом при сравнении эффективности различных вариантов модельных расчётов. Здесь для простоты изложения трудовые ресурсы и основные фонды не разделялись по их видам. Учёт последнего приводит к более сложным моделям. Рассмотрим одну из них.
Расширенная модель МОБ Выделим из вектора конечного продукта фонд производственного накопления в виде прироста основных фондов DФ, тогда Y = где Y – конечный продукт статистической модели МОБ; Тогда система (2.6) запишется Х = АХ + DФ + Дополним её системой балансов основных фондов, устанавливающей равенство ресурсов и потребностей по каждому виду основных фондов в среднегодовом исчислении: где Фk – среднегодовой объём фондов kj-го вида на начало года; fkj – коэффициенты прямой фондоёмкости; Переход от величины среднегодового ввода в действие основных фондов к абсолютному и обратно осуществляется с помощью коэффициентов равномерности ввода в действие основных фондов lk : С учётом этого, уравнение (2.23) в матричном виде перепишется Ф + L DФ = FX + где L – диагональная матрица коэффициентов равномерности ввода в действие основных фондов. Система уравнений распределения продукции и баланс основных фондов (2.24) вместе образуют систему уравнений расширенной модели МОБ
Решая её совместно, получим объёмы выпуска продукции Х и обеспечивающий их прирост основных фондов DФ.
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 391. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
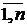 ) , (2.4)
) , (2.4)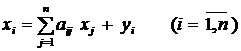 . (2.6)
. (2.6)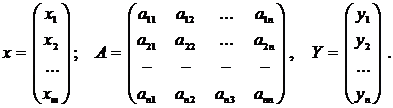
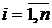 ), в противном случае производство лишается всякого смысла (если aii>1, то xii >xi). Кроме того, aij £ 1 для всех отраслей и
), в противном случае производство лишается всякого смысла (если aii>1, то xii >xi). Кроме того, aij £ 1 для всех отраслей и 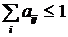 , что естественно для продуктивной экономики, иначе отрасль будет настолько убыточной, что её убытки перекроют расходы на амортизацию и оплату труда.
, что естественно для продуктивной экономики, иначе отрасль будет настолько убыточной, что её убытки перекроют расходы на амортизацию и оплату труда.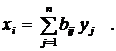 (2.11)
(2.11)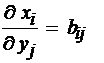 или
или 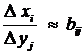 . Отсюда имеем, что bij показывает потребность в дополнительном валовом выпуске продукции i-й отрасли для производства дополнительной единицы конечной продукции j-й отрасли. Таким образом, bij в сущности есть мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию.
. Отсюда имеем, что bij показывает потребность в дополнительном валовом выпуске продукции i-й отрасли для производства дополнительной единицы конечной продукции j-й отрасли. Таким образом, bij в сущности есть мультипликатор, показывающий эффект распространения спроса на валовую продукцию, первоначальным источником которого является спрос на конечную продукцию.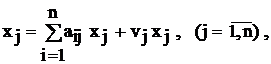
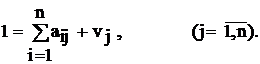 (2.12)
(2.12)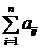 показывает возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации). Система равенств (2.12) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.
показывает возмещение стоимости, а vj – вновь созданную стоимость (с учётом амортизации). Система равенств (2.12) представляет собой модель балансовых цен, на основе которой можно выяснить, как через посредство структуры потребляемых каждой отраслью ресурсов изменяется структура цен при варьировании величины добавленной стоимости.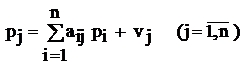 . (2.13)
. (2.13)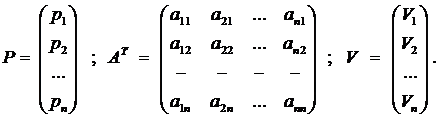
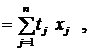 (2.16)
(2.16)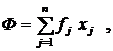 (2.17)
(2.17)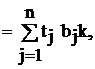 (2.20)
(2.20)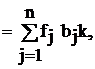 (2.21)
(2.21)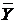 + DФ,
+ DФ,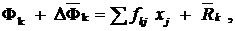 (2.23)
(2.23) 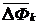 – среднегодовой ввод фондов k-го вида;
– среднегодовой ввод фондов k-го вида;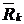 – среднегодовое выбытие фондов k-го вида.
– среднегодовое выбытие фондов k-го вида.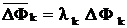 .
.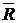 , (2.24)
, (2.24)