
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Производственно-транспортные задачи
Решение производственно-транспортных задач основывается на решении классической транспортной задачи по критерию минимума целевой функции (т/км, руб.) с учётом суммарных затрат на производство и доставку однородной продукции до потребителей. Транспортная задача по критерию издержек
Постановка задачи: На m станциях отправления А1, А2, ..., Аi, ..., Аm имеется a1, а2, ..., аi, ..., аm единиц однородного груза соответственно. Этот груз необходимо перевезти n потребителям В1, В2, ..., Вj, ..., Bn в количествах, соответственно равных b1, b2, ..., bj, ..., bn. Известны величины Сij, характеризующие затраты по перевозке единицы груза из пункта Аi в пункт Bj. Требуется определить оптимальный план перевозок, при котором минимизируются общие суммарные затраты на перевозки. Математическая модель задачи. Пусть xij – объём перевозки груза из пункта Аi в пункт Bj (от i-гo поставщика до j-гo потребителя), тогда Система ограничений (4.26) характеризует ограничения по ресурсам, (4.27) –ограничения по потребностям. Составим таблицу для решения данной задачи (таблица 4.2).
Если для задачи (4.26) – (4.28) выполнено условие баланса то транспортная задача называется закрытой. Если условие баланса не выполняется, то задача называется открытой. Задача приводится к закрытой введением фиктивного поставщика с мощностью Необходимое и достаточное условие для разрешимости задачи сводится к выполнению условия баланса (4.29). Исходный опорный план можно найти по методу северо-западного угла или минимального элемента. Невырожденный план задачи содержит (m + n – 1) базисных переменных, которым соответствуют занятые клетки в таблице решения. Решение задачи обычно находится по методу потенциалов, который основывается на следующей теореме. Теорема о потенциалах. Если план х* = (хij*) транспортной задачи (4.26) – (4.28) является оптимальным, то ему соответствует система из (m + n) чисел Ui* и Vj*, удовлетворяющих условиям: 1) Ui* + Vj* = Сij, для хij* > 0; (4.30) 2) Ui* + Vj* ≤ Сij, для хij* = 0; (4.31) Из условия (3.31) получается, что в оптимальном плане для свободных клеток Eij = Сij – (Ui* + Vj*) ≥ 0. Числа Eij называются характеристиками свободных клеток (i, j). Eij показывает, насколько изменится значение целевой функции при перемещении в клетку (i, j) единицы груза. Если в оптимальном плане для свободных клеток Eij = 0, то оптимальный план не единственный.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 359. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
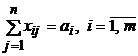 ; (4.26)
; (4.26)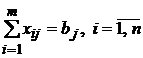 ; (4.27)
; (4.27)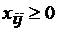 ;
;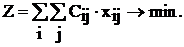 (4.28)
(4.28)









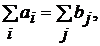 (4.29)
(4.29)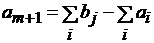 (если
(если 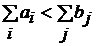 ) или фиктивного потребителя со спросом
) или фиктивного потребителя со спросом 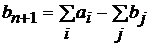 (если
(если 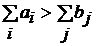 ). Для фиктивного поставщика или потребителя Сij = 0.
). Для фиктивного поставщика или потребителя Сij = 0.