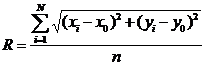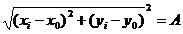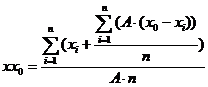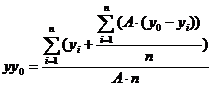Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Обработка результатов измерений при измерении отклонения от круглости.⇐ ПредыдущаяСтр 12 из 12 При оценке некруглости детали с приблизительно равными основаниями можно воспользоваться одним из четырех вариантов: наружной прилегающей окружностью, внутренней прилегающей окружностью, средней окружностью и кольцевой зоной минимальной ширины
На круглограмме такая окружность будет представлена окружностью, описанной вокруг круглограммы, причем диаметр этой окружности должен быть минимален. Отклонение от круглости определится как разность между наибольшим и наименьшим радиусами-векторами круглограммы относительно центра наружной прилегающей окружности. Внутренней прилегающей называется окружность наибольшего возможного диаметра, вписанная в реальный профиль. На диаграмме ее представляет окружность, вписанная в круглограмму, причем диаметр этой окружности максимален. Отклонение от круглости, в этом случае, равно разности наибольшего и наименьшего радиусов круглограммы, проведенных из центра внутренней прилегающей окружности.
Кольцевой зоной наименьшей ширины называется зона, образованная двумя концентричными окружностями, охватывающими кривую профиля или круглограмму извне и изнутри, причем центр этих окружностей расположен таким образом, что радиальное расстояние между ними минимально. Ширина зоны определяет отклонение от круглости. 
Каждый из рассматриваемых вариантов базовой окружности имеет свои достоинства и недостатки. С точки зрения физического смысла один из них не является оптимальным для всех возможных случаев контроля круглости. Прилегающие окружности наиболее удобны при оценке формы деталей предназначенных для работы в подвижных соединениях. Они имеют в этих случаях наглядный физический смысл, так как воспроизводят элемент идеальной поверхности, сопряженной с проверяемой. В прессовых соединениях важно знать распределение материала детали относительно окружности среднего диаметра, так как от равномерности этого распределения зависит прочность посадки. В таком случае оптимальным вариантом базовой окружности является средняя окружность. Можно найти случаи, когда оптимальной представляется система кольцевой зоны минимальной ширины. Один из них — оценка некруглости линий — траекторий движения, следов пересечения двух поверхностей и т. п. При этом в зависимости от метода измерения круглости различия в ее величине не превышают 10%, а потому для анализа можно пользоваться любым способом. Однако наиболее подходящим для измерения круглости при помощи ЭВМ является метод измерения отклонений от средней окружности. В этом случае отклонение от круглости соответствует размаху развертки реального профиля, который можно легко измерить при проведении исследований. Овальность можно оценить как наибольшую полуразность взаимно перпендикулярных диаметров реального профиля. Для построения базовой окружности необходимо знать координаты ее центра и величину радиуса. Как показал Спрэгг, параметры средней окружности могут быть определены в полярной системе координат по уравнениям:
|
||
|
Последнее изменение этой страницы: 2018-06-01; просмотров: 426. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
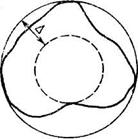 Наружной прилегающей окружностью согласно ГОСТ 10356 – 63 называется окружность наименьшего возможного диаметра, описанная вокруг реального профиля.
Наружной прилегающей окружностью согласно ГОСТ 10356 – 63 называется окружность наименьшего возможного диаметра, описанная вокруг реального профиля.
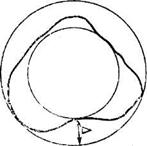 Средней окружностью называется окружность, проведенная относительно кривой профиля или круглограммы таким образом, что сумма квадратов расстояний от этой окружности до кривой является минимальной. Отклонение от круглости определяется при этом как разность наибольшего и наименьшего радиусов-векторов круглограммы, проведенных из центра средней окружности.
Средней окружностью называется окружность, проведенная относительно кривой профиля или круглограммы таким образом, что сумма квадратов расстояний от этой окружности до кривой является минимальной. Отклонение от круглости определяется при этом как разность наибольшего и наименьшего радиусов-векторов круглограммы, проведенных из центра средней окружности.