
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема лекции № 4 Нелинейные эконометрические модели.Конспект лекции: Если между экономическими явлениями существуют нелинейные соотношения, то они выражаются с помощью соответствующих нелинейных функций. Различают два класса нелинейных регрессий: 1. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам, например – полиномы различных степеней – – равносторонняя гипербола – – полулогарифмическая функция – 2. Регрессии, нелинейные по оцениваемым параметрам, например – степенная – – показательная – – экспоненциальная – Регрессии нелинейные по включенным переменным приводятся к линейному виду простой заменой переменных, а дальнейшая оценка параметров производится с помощью метода наименьших квадратов. Рассмотрим некоторые функции. Парабола второй степени А после обратной замены переменных получим Парабола второй степени обычно применяется в случаях, когда для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. Равносторонняя гипербола  Аналогичным образом приводятся к линейному виду зависимости Несколько иначе обстоит дело с регрессиями нелинейными по оцениваемым параметрам, которые делятся на два типа: нелинейные модели внутренне линейные (приводятся к линейному виду с помощью соответствующих преобразований, например, логарифмированием) и нелинейные модели внутренне нелинейные (к линейному виду не приводятся). К внутренне линейным моделям относятся, например, степенная функция –
К внутренне нелинейным моделям можно, например, отнести следующие модели: Среди нелинейных моделей наиболее часто используется степенная функция где а затем потенцированием находим искомое уравнение. Широкое использование степенной функции связано с тем, что параметр b в ней имеет четкое экономическое истолкование – он является коэффициентом эластичности. (Коэффициент эластичности показывает, на сколько процентов измениться в среднем результат, если фактор изменится на 1%.) Формула для расчета коэффициента эластичности имеет вид: Так как для остальных функций коэффициент эластичности не является постоянной величиной, а зависит от соответствующего значения фактора x , то обычно рассчитывается средний коэффициент эластичности: Приведем формулы для расчета средних коэффициентов эластичности для наиболее часто используемых типов уравнений регрессии: Таблица 2 Возможны случаи, когда расчет коэффициента эластичности не имеет смысла. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения в процентах. Уравнение нелинейной регрессии, так же, как и в случае линейной зависимости, дополняется показателем тесноты связи. В данном случае это индекс корреляции: Где Величина данного показателя находится в пределах: т.е. имеет тот же смысл, что и в линейной регрессии; Индекс детерминации Индекс детерминации используется для проверки существенности в целом уравнения регрессии по F -критерию Фишера: где О качестве нелинейного уравнения регрессии можно также судить и по средней ошибке аппроксимации, которая, так же как и в линейном случае. Производственная функция Кобба-Дугласа. Макроэкономическая производственная функция – это статистически значимая связь между объемом выпуска У, капитальными затратами К и затратами труда L. Для моделирования и решение задач как на макро, так и на микроэкономическом уровне часто используют производственную функцию Кобба-Дугласа(КД)
где А, α,β –параметры функции , причем А>0; 0<α<1; 0<β<1, ε-случайный член. В 1927г Пол Дуглас, экономист обнаружил, что если нанести на одну и ту же диаграмму графики логарифмов показателей реального объема выпускаУ, капитальных затрат К и затрат труда L, то расстояние от точек до точек графиков показателей затрат труда и капитала будут составлять постоянную пропорцию. Математик Чарльз Кобб определил математическую зависимость, обладающую такой особенностью и предложил функцию При построении функции КД с использованием данных временного ряда следует иметь в виду, что на выпуск продукции оказывает также влияние технического прогресса. Влияние технического прогресса можно учесть, записав функцию КД в виде Свойства производственной функции Кобба-Дугласа. 1) Эластичность выпуска продукции. Эластичность выпуска продукции по капиталу и труду равна соответственно α и β: Это означает, что увеличение затрат капитала на 1% приведет к росту выпуска продукции на α%, а увеличение затрат труда на 1% приведет к росту выпуска на β%. 2) Эффект от масштаба производства. При росте затрат каждого из факторов K,L в λ раз выпуск возрастает в Это означает следующее: - если α+β>1, то функция КД имеет возрастающую отдачу от масштаба производства; - если α+β<1, то функции КД имеет убывающую отдачу от масштаба производства; - если α+β=1, то функция КД имеет постоянную отдачу от масштаба производства. 3) Прогнозируемые доли производственных факторов. В рыночной экономике оценки α и β интерпретируют как прогнозируемые доли дохода, полученные соответственно за счет капитала и труда. Для оценки параметров производственной функции КД с помощью модели множественной линейной регрессии прологарифмируем функцию При этом предполагается, что ошибки lnε обладают свойствами, необходимыми для оценивания линейной регрессионной модели. По рядам данных У, К, L рассчитываются ряды их логарифмов и для них оценивается уравнение регрессии.
Основная литература:1[53-70], 7[80-89] Дополнительная литература:6[33-34], 4[71-78] Контрольные вопросы: 1.Приведите нелинейное уравнение 2. Каким путем можно устранить нелинейность по параметру? 3. Какие виды функции, вы знаете? 4. В каких случаях используют производственную функцию и почему? 5. Перечислите свойства производственной функции Кобба-Дугласа. 6. Коэффициенты эластичности для разных видов регрессионных моделей. 7. Корреляция и F -критерий Фишера для нелинейной регрессии.
Тема лекции № 5. Множественная регрессия и корреляция. Метод наименьших квадратов (МНК).Свойства оценок на основе МНК. Качество оценивания: коэффициент Конспект лекции: Множественная регрессия и корреляция Парная регрессия может дать хороший результат при моделировании, если влиянием других факторов, воздействующих на объект исследования, можно пренебречь. Если же этим влиянием пренебречь нельзя, то в этом случае следует попытаться выявить влияние других факторов, введя их в модель, т.е. построить уравнение множественной регрессии где y – зависимая переменная (результативный признак), В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель. Спецификация модели. Отбор факторов при построении уравнения множественной регрессии Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели. Он включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Включение в уравнение множественной регрессии того или иного набора факторов связано прежде всего с представлением исследователя о природе взаимосвязи моделируемого показателя с другими экономическими явлениями. Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям. 1. Они должны быть количественно измеримы. Если необходимо включить в модель качественный фактор, не имеющий количественного измерения, то ему нужно придать количественную определенность. 2. Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи. Включение в модель факторов с высокой интеркорреляцией, может привести к нежелательным последствиям – система нормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов регрессии. Если между факторами существует высокая корреляция, то нельзя определить их изолированное влияние на результативный показатель и параметры уравнения регрессии оказываются неинтерпретируемыми. Включаемые во множественную регрессию факторы должны объяснить вариацию независимой переменной. Если строится модель с набором m факторов, то для нее рассчитывается показатель детерминации При дополнительном включении в регрессию m+1 фактора коэффициент детерминации должен возрастать, а остаточная дисперсия уменьшаться: Если же этого не происходит и данные показатели практически не отличаются друг от друга, то включаемый в анализ фактор Насыщение модели лишними факторами не только не снижает величину остаточной дисперсии и не увеличивает показатель детерминации, но и приводит к статистической незначимости параметров регрессии по критерию Стьюдента. Таким образом, хотя теоретически регрессионная модель позволяет учесть любое число факторов, практически в этом нет необходимости. Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют статистики для параметров регрессии. Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если Предпочтение при этом отдается не фактору, более тесно связанному с результатом, а тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами. В этом требовании проявляется специфика множественной регрессии как метода исследования комплексного воздействия факторов в условиях их независимости друг от друга. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Включение в модель мультиколлинеарных факторов нежелательно в силу следующих последствий: 1. Затрудняется интерпретация параметров множественной регрессии как характеристик действия факторов в «чистом» виде, ибо факторы коррелированы; параметры линейной регрессии теряют экономический смысл. 2. Оценки параметров ненадежны, обнаруживают большие стандартные ошибки и меняются с изменением объема наблюдений (не только по величине, но и по знаку), что делает модель непригодной для анализа и прогнозирования. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Если бы факторы не коррелировали между собой, то матрица парных коэффициентов корреляции между факторами была бы единичной матрицей, поскольку все недиагональные элементы матрица коэффициентов корреляции между факторами имела бы определитель, равный единице: Если же, наоборот, между факторами существует полная линейная зависимость и все коэффициенты корреляции равны единице, то определитель такой матрицы равен нулю: Чем ближе к нулю определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И, наоборот, чем ближе к единице определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Существует ряд подходов преодоления сильной межфакторной корреляции. Самый простой путь устранения мультиколлинеарности состоит в исключении из модели одного или нескольких факторов. Другой подход связан с преобразованием факторов, при котором уменьшается корреляция между ними. Одним из путей учета внутренней корреляции факторов является переход к совмещенным уравнениям регрессии, т.е. к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие. Так, если y=f(x1,x2,x3), то возможно построение следующего совмещенного уравнения: Рассматриваемое уравнение включает взаимодействие первого порядка (взаимодействие двух факторов). Возможно включение в модель и взаимодействий более высокого порядка, если будет доказана их статистическая значимость по F -критерию Фишера, но, как правило, взаимодействия третьего и более высоких порядков оказываются статистически незначимыми. Отбор факторов, включаемых в регрессию, является одним из важнейших этапов практического использования методов регрессии. Подходы к отбору факторов на основе показателей корреляции могут быть разные. Они приводят построение уравнения множественной регрессии соответственно к разным методикам. В зависимости от того, какая методика построения уравнения регрессии принята, меняется алгоритм ее решения на ЭВМ. Наиболее широкое применение получили следующие методы построения уравнения множественной регрессии: 1. Метод исключения – отсев факторов из полного его набора. 2. Метод включения – дополнительное введение фактора. 3. Шаговый регрессионный анализ – исключение ранее введенного фактора. При отборе факторов также рекомендуется пользоваться следующим правилом: число включаемых факторов обычно в 6–7 раз меньше объема совокупности, по которой строится регрессия. Если это соотношение нарушено, то число степеней свободы остаточной дисперсии очень мало. Это приводит к тому, что параметры уравнения регрессии оказываются статистически незначимыми, а F –критерий меньше табличного значения. Метод наименьших квадратов (МНК). Свойства оценок на основе МНК. Возможны разные виды уравнений множественной регрессии: линейные и нелинейные. Ввиду четкой интерпретации параметров наиболее широко используется линейная функция. В линейной множественной регрессии параметры при x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизмененном значении других факторов, закрепленных на среднем уровне. Рассмотрим линейную модель множественной регрессии Классический подход к оцениванию параметров линейной модели множественной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных

Как известно из курса математического анализа, для того чтобы найти экстремум функции нескольких переменных, надо вычислить частные производные первого порядка по каждому из параметров и приравнять их к нулю. Итак. Имеем функцию m +1 аргумента: Находим частные производные первого порядка: После элементарных преобразований приходим к системе линейных нормальных уравнений для нахождения параметров линейного уравнения множественной регрессии (30):

Для двухфакторной модели данная система будет иметь вид: Метод наименьших квадратов применим и к уравнению множественной регрессии в стандартизированном масштабе:
Стандартизованные коэффициенты регрессии показывают, на сколько единиц изменится в среднем результат, если соответствующий фактор В силу того, что все переменные заданы как центрированные и нормированные, стандартизованные коэффициенты регрессии Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе, получим систему нормальных уравнений вида

где Коэффициенты «чистой» регрессии

Поэтому можно переходить от уравнения регрессии в стандартизованном масштабе (33) к уравнению регрессии в натуральном масштабе переменных (30), при этом параметр a определяется как Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов – из модели исключаются факторы с наименьшим значением На основе линейного уравнения множественной регрессии

могут быть найдены частные уравнения регрессии:

т.е. уравнения регрессии, которые связывают результативный признак с соответствующим фактором
При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парных уравнений линейной регрессии, т.е. имеем

где
Где
которые показывают на сколько процентов в среднем изменится результат, при изменении соответствующего фактора на 1%. Средние показатели эластичности можно сравнивать друг с другом и соответственно ранжировать факторы по силе их воздействия на результат. Проверка существенности факторов и показатели качества регрессии Практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – показателя детерминации. Показатель множественной корреляции характеризует тесноту связи рассматриваемого набора факторов с исследуемым признаком или, иначе, оценивает тесноту совместного влияния факторов на результат. Независимо от формы связи показатель множественной корреляции может быть найден как индекс множественной корреляции:

где Границы изменения индекса множественной корреляции от 0 до 1. Чем ближе его значение к 1, тем теснее связь результативного признака со всем набором исследуемых факторов. Величина индекса множественной корреляции должна быть больше или равна максимальному парному индексу корреляции: При правильном включении факторов в регрессионную модель величина индекса множественной корреляции будет существенно отличаться от индекса корреляции парной зависимости. Если же дополнительно включенные в уравнение множественной регрессии факторы третьестепенны, то индекс множественной корреляции может практически совпадать с индексом парной корреляции (различия в третьем, четвертом знаках). Отсюда ясно, что сравнивая индексы множественной и парной корреляции, можно сделать вывод о целесообразности включения в уравнение регрессии того или иного фактора. Расчет индекса множественной корреляции предполагает определение уравнения множественной регрессии и на его основе остаточной дисперсии:

Можно пользоваться следующей формулой индекса множественной детерминации:

где Формула индекса множественной корреляции для линейной регрессии получила название линейного коэффициента множественной корреляции, или, что то же самое, совокупного коэффициента корреляции. Возможно также при линейной зависимости определение совокупного коэффициента корреляции через матрицу парных коэффициентов корреляции:
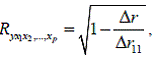
где – определитель матрицы парных коэффициентов корреляции; – определитель матрицы межфакторной корреляции. Как видим, величина множественного коэффициента корреляции зависит не только от корреляции результата с каждым из факторов, но и от межфакторной корреляции. Рассмотренная формула позволяет определять совокупный коэффициент корреляции, не обращаясь при этом к уравнению множественной регрессии, а используя лишь парные коэффициенты корреляции. В рассмотренных показателях множественной корреляции (индекс и коэффициент) используется остаточная дисперсия, которая имеет систематическую ошибку в сторону преуменьшения, тем более значительную, чем больше параметров определяется в уравнении регрессии при заданном объеме наблюдений n . Если число параметров при Для того чтобы не допустить возможного преувеличения тесноты связи, используется скорректированный индекс (коэффициент) множественной корреляции. Скорректированный индекс множественной корреляции содержит поправку на число степеней свободы, а именно остаточная сумма квадратов (n- m-1), а общая сумма квадратов отклонений Формула скорректированного индекса множественной детерминации имеет вид:
 , ,
где m – число параметров при переменных x ; n – число наблюдений. Поскольку
 , то величину скорректированного индекса детерминации можно представить в виде: , то величину скорректированного индекса детерминации можно представить в виде:
Чем больше величина m, тем сильнее различия Как было показано выше, ранжирование факторов, участвующих во множественной линейной регрессии, может быть проведено через стандартизованные коэффициенты регрессии (β-коэффициенты). Эта же цель может быть достигнута с помощью частных коэффициентов корреляции (для линейных связей). Кроме того, частные показатели корреляции широко используются при решении проблемы отбора факторов: целесообразность включения того или иного фактора в модель можно доказать величиной показателя частной корреляции. Частные коэффициенты корреляции характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании (устранении влияния) других факторов, включенных в уравнение регрессии. Показатели частной корреляции представляют собой отношение сокращения остаточной дисперсии за счет дополнительного включения в анализ нового фактора к остаточной дисперсии, имевшей место до введения его в модель. В общем виде при наличии m факторов для уравнения Где При двух факторах формула (48) примет вид:

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например,

При двух факторах данная формула примет вид:
 . .
Для уравнения регрессии с тремя факторами частные коэффициенты корреляции второго порядка определяются на основе частных коэффициентов корреляции первого порядка. Так, по уравнению

Рассчитанные по рекуррентной формуле частные коэффициенты корреляции изменяются в пределах от –1 до +1, а по формулам через множественные коэффициенты детерминации – от 0 до 1. Сравнение их друг с другом позволяет ранжировать факторы по тесноте их связи с результатом. Частные коэффициенты корреляции дают меру тесноты связи каждого фактора с результатом в чистом виде. Если из стандартизованного уравнения регрессии В эконометрике частные коэффициенты корреляции обычно не имеют самостоятельного значения. Их используют на стадии формирования модели. Так, строя многофакторную модель, на первом шаге определяется уравнение регрессии с полным набором факторов и рассчитывается матрица частных коэффициентов корреляции. На втором шаге отбирается фактор с наименьшей и несущественной по t –критерию Стьюдента величиной показателя частной корреляции. Исключив его из модели, строится новое уравнение регрессии. Процедура продолжается до тех пор, пока не окажется, что все частные коэффициенты корреляции существенно отличаются от нуля. Если исключен несущественный фактор, то множественные коэффициенты детерминации на двух смежных шагах построения регрессионной модели почти не отличаются друг от друга, Из приведенных выше формул частных коэффициентов корреляции видна связь этих показателей с совокупным коэффициентом корреляции. Зная частные коэффициенты корреляции (последовательно первого, второго и более высокого порядка), можно определить совокупный коэффициент корреляции по формуле:

В частности, для двухфакторного уравнения формула (51) принимает вид:

При полной зависимости результативного признака от исследуемых факторов коэффициент совокупного их влияния равен единице. Из единицы вычитается доля остаточной вариации результативного признака Значимость уравнения множественной регрессии в целом, так же как и в парной регрессии, оценивается с помощью F -критерия Фишера:

где Оценивается значимость не только уравнения в целом, но и фактора, дополнительно включенного в регрессионную модель. Необходимость такой оценки связана с тем, что не каждый фактор, вошедший в модель, может существенно увеличивать долю объясненной вариации результативного признака. Кроме того, при наличии в модели нескольких факторов они могут вводиться в модель в разной последовательности. Ввиду корреляции между факторами значимость одного и того же фактора может быть разной в зависимости от последовательности его введения в модель. Мерой для оценки включения фактора в модель служит частный F -критерий, т.е. Частный F- критерий построен на сравнении прироста факторной дисперсии, обусловленного влиянием дополнительно включенного фактора, с остаточной дисперсией на одну степень свободы по регрессионной модели в целом. В общем виде для фактора

Где
 превышает превышает  , то дополнительное включение фактора , то дополнительное включение фактора  в модель статистически оправданно и коэффициент чистой регрессии в модель статистически оправданно и коэффициент чистой регрессии  при факторе при факторе  статистически значим. Если же фактическое значение статистически значим. Если же фактическое значение  меньше табличного, то дополнительное включение в модель фактора меньше табличного, то дополнительное включение в модель фактора  не увеличивает существенно долю объясненной вариации признака y, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим. Для двухфакторного уравнения частные F -критерии имеют вид: не увеличивает существенно долю объясненной вариации признака y, следовательно, нецелесообразно его включение в модель; коэффициент регрессии при данном факторе в этом случае статистически незначим. Для двухфакторного уравнения частные F -критерии имеют вид:
С помощью частного F -критерия можно проверить значимость всех коэффициентов регрессии в предположении, что каждый соответствующий фактор
 , можно определить и t -критерий для коэффициента регрессии при i -м факторе, , можно определить и t -критерий для коэффициента регрессии при i -м факторе,  , а именно: , а именно: 
Оценка значимости коэффициентов чистой регрессии по t -критерию Стьюдента может быть проведена и без расчета частных F –критериев. В этом случае, как и в парной регрессии, для каждого фактора используется формула:

где Для уравнения множественной регрессии

Где Как видим, чтобы воспользоваться данной формулой, необходимы матрица межфакторной корреляции и расчет по ней соответствующих коэффициентов детерминации детерминации Взаимосвязь показателей частного коэффициента корреляции, частного F -критерия и t -критерия Стьюдента для коэффициентов чистой регрессии может использоваться в процедуре отбора факторов. Отсев факторов при построении уравнения регрессии методом исключения практически можно осуществлять не только по частным коэффициентам корреляции, исключая на каждом шаге фактор с наименьшим незначимым значением частного коэффициента корреляции, но и по величинам
Основная литература :[85-96] Дополнительная литература:3[60-65] Контрольные вопросы: 1. Приведите уравнение множественной линейной регрессии. 2. Отбор факторов при построении уравнения множественной регрессии. 3. Оценка параметров уравнения множественной регрессии. 4. Множественная корреляция. 5. Частные коэффициенты корреляции. 6. F -критерий Фишера и частный F -критерий Фишера для уравнения множественной регрессии. 7. t -критерий Стьюдента для уравнения множественной регрессии.
Тема лекции № 6. Линейные регрессионные модели с гетероскедастичными остатками. Конспект лекции: При оценке параметров уравнения регрессии применяется метод наименьших квадратов (МНК). При этом делаются определенные предпосылки относительно случайной составляющей ε. В модели случайная составляющая ε представляет собой ненаблюдаемую величину. После того как произведена оценка параметров модели, рассчитывая разности фактических и теоретических значений результативного признака y, можно определить оценки случайной составляющей При изменении спецификации модели, добавлении в нее новых наблюдений выборочные оценки остатков При использовании критериев Фишера и Стьюдента делаются предположения относительно поведения остатков Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям. Они должны быть несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков. Поэтому очень важно исследовать поведение остаточных величин регрессии Исследования остатков 1) случайный характер остатков; 2) нулевая средняя величина остатков, не зависящая от 3) гомоскедастичность – дисперсия каждого отклонения 4) отсутствие автокорреляции остатков – значения остатков 5) остатки подчиняются нормальному распределению. Если распределение случайных остатков Прежде всего, проверяется случайный характер остатков Рисунок 4.Зависимость случайных остатков Возможны следующие случаи, если 1) остатки 2) остатки 3) остатки В этих случаях необходимо либо применять другую функцию, либо вводить дополнительную информацию и заново строить уравнение регрессии до тех пор, пока остатки |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 560. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ,
,  ;
; ;
;
 ;
; ;
; .
. приводится к линейному виду с помощью замены:
приводится к линейному виду с помощью замены:  . В результате приходим к двухфакторному уравнению
. В результате приходим к двухфакторному уравнению  , оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:
, оценка параметров которого при помощи МНК, приводит к системе следующих нормальных уравнений:

 может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы, расходов на непродовольственные товары от доходов или общей суммы расходов и в других случаях. Гипербола приводится к линейному уравнению простой заменой:
может быть использована для характеристики связи удельных расходов сырья, материалов, топлива от объема выпускаемой продукции, времени обращения товаров от величины товарооборота, процента прироста заработной платы от уровня безработицы, расходов на непродовольственные товары от доходов или общей суммы расходов и в других случаях. Гипербола приводится к линейному уравнению простой заменой:  . Система линейных уравнений при применении МНК будет выглядеть следующим образом:
. Система линейных уравнений при применении МНК будет выглядеть следующим образом:
 и другие.
и другие. , показательная –
, показательная –  , экспоненциальная –
, экспоненциальная –  , логистическая –
, логистическая –  , обратная –
, обратная – 

 , которая приводится к линейному виду логарифмированием:
, которая приводится к линейному виду логарифмированием:
 , X =lnx, A=lna, Е=lnε. т.е. МНК мы применяем для преобразованных данных:
, X =lnx, A=lna, Е=lnε. т.е. МНК мы применяем для преобразованных данных:
 (26)
(26) (27)
(27)

 – общая дисперсия результативного признака y ,
– общая дисперсия результативного признака y , – остаточная дисперсия.
– остаточная дисперсия. . Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака:
. Чем ближе значение индекса корреляции к единице, тем теснее связь рассматриваемых признаков, тем более надежно уравнение регрессии. Квадрат индекса корреляции носит название индекса детерминации и характеризует долю дисперсии результативного признака y, объясняемую регрессией, в общей дисперсии результативного признака: (28)
(28)
 можно сравнивать с коэффициентом детерминации
можно сравнивать с коэффициентом детерминации  для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина
для обоснования возможности применения линейной функции. Чем больше кривизна линии регрессии, тем величина  (29)
(29) (для остаточной суммы квадратов) и
(для остаточной суммы квадратов) и  (для факторной суммы квадратов).
(для факторной суммы квадратов). ,
, . Такая функция приблизительно равна 30 годами раньше Филиппом Уикстидом, но Кобб и Дуглас первыми использовали эмпирические данные для ее построения.
. Такая функция приблизительно равна 30 годами раньше Филиппом Уикстидом, но Кобб и Дуглас первыми использовали эмпирические данные для ее построения. , где t-время, r-темп прироста выпуска, благодаря техническому прогрессу.
, где t-время, r-темп прироста выпуска, благодаря техническому прогрессу. ;
;  .
. раз.
раз. .
. .
. ,
, , который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии m факторов. Влияние других, не учтенных в модели факторов, оценивается как 1-
, который фиксирует долю объясненной вариации результативного признака за счет рассматриваемых в регрессии m факторов. Влияние других, не учтенных в модели факторов, оценивается как 1-  .
. и
и 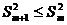 .
.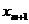 не улучшает модель и практически является лишним фактором.
не улучшает модель и практически является лишним фактором. . Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии.
. Если факторы явно коллинеарны, то они дублируют друг друга и один из них рекомендуется исключить из регрессии. (i≠ j ) были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных
(i≠ j ) были бы равны нулю. Так, для уравнения, включающего три объясняющих переменных

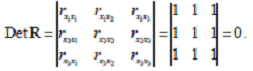


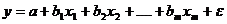 (30)
(30) минимальна:
минимальна:



 – стандартизированные переменные:
– стандартизированные переменные:  ,
,  , для которых среднее значение равно нулю:
, для которых среднее значение равно нулю:  , а среднее квадратическое отклонение равно единице:
, а среднее квадратическое отклонение равно единице:  ;
;  – стандартизированные коэффициенты регрессии.
– стандартизированные коэффициенты регрессии. и
и  коэффициенты парной и межфакторной корреляции.
коэффициенты парной и межфакторной корреляции. .
.


 – частное уравнение регрессии.
– частное уравнение регрессии.
 – общая дисперсия результативного признака;
– общая дисперсия результативного признака;  – остаточная дисперсия.
– остаточная дисперсия.

 –парные коэффициенты корреляции результата с каждым фактором.
–парные коэффициенты корреляции результата с каждым фактором.

 делится на число степеней свободы остаточной вариации
делится на число степеней свободы остаточной вариации  на число степеней свободы в целом по совокупности (n-1).
на число степеней свободы в целом по совокупности (n-1).
 и
и  коэффициент частной корреляции, измеряющий влияние на y фактора
коэффициент частной корреляции, измеряющий влияние на y фактора 
 – множественный коэффициент детерминации всех m факторов с результатом;
– множественный коэффициент детерминации всех m факторов с результатом;  – тот же показатель детерминации, но без введения в модель фактора
– тот же показатель детерминации, но без введения в модель фактора  –коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле:
–коэффициент частной корреляции первого порядка. Соответственно коэффициенты парной корреляции называются коэффициентами нулевого порядка. Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле: возможно исчисление трех частных коэффициентов корреляции второго порядка:
возможно исчисление трех частных коэффициентов корреляции второго порядка: каждый из которых определяется по рекуррентной формуле. Например, при i=1 имеем формулу для расчета
каждый из которых определяется по рекуррентной формуле. Например, при i=1 имеем формулу для расчета 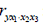
 следует, что
следует, что  , т.е. пo силе влияния на результат порядок факторов таков:
, т.е. пo силе влияния на результат порядок факторов таков:  , то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции,
, то этот же порядок факторов определяется и по соотношению частных коэффициентов корреляции, , где m – число факторов.
, где m – число факторов. , обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов.
, обусловленная последовательно включенными в анализ факторами. В результате подкоренное выражение характеризует совокупное действие всех исследуемых факторов. – факторная сумма квадратов на одну степень свободы;
– факторная сумма квадратов на одну степень свободы;  –остаточная сумма квадратов на одну степень свободы;
–остаточная сумма квадратов на одну степень свободы;  – коэффициент множественной детерминации для модели с полным набором факторов,
– коэффициент множественной детерминации для модели с полным набором факторов,  – тот же показатель, но без включения в модель фактора
– тот же показатель, но без включения в модель фактора 
 – средняя квадратическая (стандартная) ошибка коэффициента регрессии
– средняя квадратическая (стандартная) ошибка коэффициента регрессии  средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле:
средняя квадратическая ошибка коэффициента регрессии может быть определена по следующей формуле: – среднее квадратическое отклонение для признака y ,
– среднее квадратическое отклонение для признака y ,  – среднее квадратическое отклонение для признака
– среднее квадратическое отклонение для признака  –коэффициент детерминации для уравнения множественной регрессии,
–коэффициент детерминации для уравнения множественной регрессии, 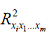 – коэффициент детерминации для зависимости фактора
– коэффициент детерминации для зависимости фактора  . Так, для уравнения
. Так, для уравнения 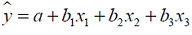 оценка значимости коэффициентов регрессии
оценка значимости коэффициентов регрессии  предполагает расчет трех межфакторных коэффициентов
предполагает расчет трех межфакторных коэффициентов :
: . Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е.
. Поскольку они не являются реальными случайными остатками, их можно считать некоторой выборочной реализацией неизвестного остатка заданного уравнения, т.е.  .
.
 .
.