
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Числовые характеристики выборочной совокупностиПусть из генеральной совокупности извлекается выборка объема n. Считаем что выборочные наблюдения Числовыми характеристиками выборочной совокупности являются выборочная средняя и выборочная дисперсия. Выборочной средней называется среднее арифметическое значение случайной величины в выборке
Выборочной дисперсией (или вариацией) называется среднее арифметическое квадратов отклонения случайной величины от ее среднего значения
Выборочную дисперсию удобно вычислять по формуле Свойства выборочной дисперсии анологичны свойствам теоретической дисперсии Стандартным или среднеквадратическим отклонением случайной величины в выборке называется величина Для разных выборок, взятых из одной и той же генеральной совокупности, выборочные средние и выборочные дисперсии будут различные, т.е. выборочные характеристики являюстя случайными величинами.
Основная литература: 1[3-7] Дополнительная литература: 5[5-6] Контрольные вопросы: 1.Дайте определение эконометрики. 2.Приведите основные типы статистических данных. 3.Дайте определение случайной величины. 4.Дайте определение математического ожидания, приведите свойства. 5. Дайте определение теоретической дисперсии, приведите ее свойства. 6. Дайте определение выборочной средней. 7. Дайте определение выборочной дисперсии. 8. Дайте определения теоретического стандартного и средне квадратического отклонения
Тема лекции № 2.Постоянная и случайная составляющие случайной переменной. Несмещенность. Эффективность. Состоятельность. Ковариация и корреляция.  Конспект лекции:Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайно составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если х – случайная переменная и m - ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом: Случайная составляющая u определяется как разность между х и m: Способы оценивания и оценки. До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности – об ее распределении вероятностей или функции плотности распределения. С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики. На практике, за исключением искусственно простых случайных величин мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности. Процедура оценивания всегда одинакова. Берется выборка из n наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики. Способ оценивания – это общее правило, или формула. Значение оценки – это конкретное число, которое меняется от выборки к выборке. Оценки как случайные величины. Несмещенность. Эффективность. Состоятельность Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х-случайная переменная и, следовательно, случайной величиной является и функции набора ее значений. Возьмем, например Мы только, что показали, что величина х а i-м наблюдении может быть разложен на две составляющие : постоянную часть m и чисто случайную составляющую Следовательно, где Отсюда можно видеть, что Величина следовательно, Таким образом, s2 зависит от чисто случайной составляющей наблюдений х в выборке. Полученная тем или иным способом оценка характеристики случайной величины сама является случайной величиной, так как она основывается на случайных реализациях переменной. Оценка характеристики случайной величины называется несмещенной, если ее математическое ожидание совпадает с теоретическим значением этой характеристики. Например, оценкой для математического ожидания Значит, Несмещенной оценкой для математического ожидания Эффективная оценка – это та, у которой дисперсия минимальна. Рассмотрим дисперсию обобщенной оценки теоретического среднего и покажем, что она минимальна в том случае, когда оба наблюдения имеют равные веса. Если наблюдения Мы уже выяснили, что для несмещенности оценки необходимо равенство единице суммы Поскольку мы хотим выбрать Итак, мы показали, что выборочное среднее имеет наименьшую дисперсию среди оценок рассматриваемого типа. Это означает, что оно имеет наиболее «сжатое» вероятностное распределение вокруг истинного среднего и, следовательно наиболее точно. Строго говоря, выборочное среднее – это наиболее эффективная оценка среди всех несмещенных оценок. Если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называетсясостоятельной. Тот факт, что при увеличении размера выборки распределение становится симметричным вокруг истинного значения, указывает на асимптотическую несмещенность. То, что в конечном счете оно превращается в единственную точку истинного значения, говорит о состоятельности оценки. Ковариация является мерой взаимосвязи между двумя переменными. Различают выборочную и теоретическую ковариацию. Если х и у – случайные величины, то теоретическая ковариация где Выборочная ковариация между х и у задается формулой: или Правила расчета ковариации. 1. Если 2. Если 3. Если 4. 5. Правила расчета теоретической ковариации анологичны правилам расчета выборочной. Связь между выборочной дисперсией и выборочной ковариацией определяется выражением, если Более точной мерой зависимости между переменными является коэффициент корреляции. Коэффициент корреляции имеет две формы – теоретическую и выборочную. Теоретический коэффициент корреляции r определяется выражением: Теоретический коэффицент кореляции паказывает тесноту линейной связи двух случайных величин и изменяется в интервале Выборочный коэффициент корреляции r определяется путем замены теоретических дисперсий и ковариации на их несмещенные оценки. Выборочный коэффицент кореляции является случайной величиной и изменяется в интервале Выборочный коэффициент корреляции r имеет максимальное значение, равное единице, которое получается при строгой линейной положительной зависимости между выборочными значениями х и у. r принимает минимальное значение равное –1, когда существует линейная отрицательная зависимость. Величинаr=0 показывает, что зависимость между наблюдениями х и у в выборке отсутствует. Случайные величины называются некоррелированными (независимыми), если их коэффицент корреляции равен нулю и коррелированными, если он отличный от нуля.
Основная литература:. 1[10-28], 7[34-48] Дополнительная литература: 4[10-27], 6[55-57] Контрольные вопросы: 1.Что такое чисто случайная составляющая u? 2.Что такое оценка? 3.Для чего нужен способ оценивания? 4.Какая оценка называется эффективной? 5.Какая оценка называется несмещенной? 6.Какая оценка называется состоятельная? 7.Что такое выборочная, теоретическая ковариация? 8.Какие две формы имеет коэффициент корреляции? 9.Правила расчета ковариации. 10. Связь между выборочными дисперсией и ковариацией? 11. Что означает r =-1; 0; 1?
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 821. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 независимы и имеют одинаковые распределения.
независимы и имеют одинаковые распределения.



 , где ε– чисто случайная составляющая.
, где ε– чисто случайная составляющая. . Из определения следует, что математическое ожидание величины ε равно нулю, а теоретическая дисперсия ε равна теоретической дисперсии х.
. Из определения следует, что математическое ожидание величины ε равно нулю, а теоретическая дисперсия ε равна теоретической дисперсии х. - оценку математического ожидания:
- оценку математического ожидания: (5)
(5) :
: (6)
(6) (7)
(7) -выборочное среднее величин
-выборочное среднее величин  - оценка теоретической дисперсии х – также является случайной переменной. Вычитая (7) из (6), имеем:
- оценка теоретической дисперсии х – также является случайной переменной. Вычитая (7) из (6), имеем: (8)
(8) .
. может служить среднее выборочное
может служить среднее выборочное 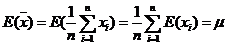 .
. является обобщенная оценка
является обобщенная оценка  при
при  (сумма весов). Это справедливо для любого числа
(сумма весов). Это справедливо для любого числа  .
. и
и  независимы, теоретическая дисперсия обобщенной оценки равна:
независимы, теоретическая дисперсия обобщенной оценки равна: (9)
(9)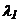 и
и  . Следовательно, для несмещенных оценок
. Следовательно, для несмещенных оценок  и
и (10)
(10) ). Минимум достигается при
). Минимум достигается при  . Следовательно,
. Следовательно,  определяется как математическое ожидание произведения отклонений этих величин от их средних значений:
определяется как математическое ожидание произведения отклонений этих величин от их средних значений:
 и
и  - теоретические средние значения х и у соответственно.
- теоретические средние значения х и у соответственно. .(11)
.(11)
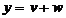 , то
, то  .
. , где а – константа, то
, где а – константа, то  .
. , где а – константа, то
, где а – константа, то  .
.
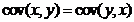
 , то
, то 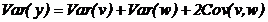 .
.

 .
.