Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Тема лекции № 1. Введение в эконометрику. Элементы теории вероятности и математической статистики.Конспект лекции:Эконометрика – наука, изучающая количественные закономерности и взаимозависимости в экономике методами математической статистики. Эконометрика с помощью статистических и математических методов анализирует экономические закономерности, доказаные экономической теорией. Эконометрический анализ служит основой для экономического анализа и прогнозирования, создавая возможность для принятия обоснованных экономических решений. Цель эконометрики – эмпирический вывод экономических законов. Задачи эконометрики – построение экономических моделей и оценивание их параметров; проверка гипотез о свойствах экономических показателей и формах их связи. Для анализа или прогноза выделяются три основных класса моделей: модели временных рядов; регрессионные модели с одним уравнением; системы одновременных уравнений. Если модель содержит только одну объясняющую переменную, т.е. k=1, она называется парной регрессией. При k>1 - множественной регрессией. Основу эконометрического моделирования составляют статистические данные, которые должны быть согласованы между собой и иметь единную методическую основу. Их различают по типам. Перекрестные данные собираются по какому-либо экономическому показателю для разных объектов (фирм, стран) в один момент времени или в разные моменты в случае, когда время несущественно. Временные ряды – данные для одного объекта в различные моменты времени. Промежуточное положение занимают панельные данные, которые отражают наблюдения по большому числу объектов за небольшое число моментов времени, например, прибыли предприятий Казахстана за последние три года.  Все значения наблюдений образуют генеральную совокупность. Часть всевозможных наблюдений генеральной совокупности называют выборочной совокупностью или выборкой. Данные выборки можно представить в виде: таблицы; диаграммы рассеяния (точки с координатами ( Случайной переменной называется переменная, которая с определенной вероятностью может принимать значения из каждого заданного множества. Различают дискретные и непрерывные случайные величины. Если случайная величина может принимать конечное или счетное число значений, то это дискретная случайная величина. Например – сумма выпавших очков при бросании двух игральных костей; чизло телевизоров, проданных в магазине за один день. Перечень возыожных значений случайной величины и соответствующих им вероятностей называется законом распределения дискретной случайной величины, который удобнее задавать в виде ряда распределения. Ряд распределения дискретной случайной величины обычно задается в виде таблицы
где При этом Закон распределения дискретной случайной величины может быть задан аналитически (в виде формулы) и графически (многоугольник распределения). Случайная величина, которая может принимать любые значения из некоторого интервала, является непрерывной случайной величиной. Например –температура в комнате; максимальный биржевой курс доллара на торгах в течение дня. Непрерывная случайная величина задается функцией плотности вероятности, принимающей неотрицательные значения. Вероятность попадания случайной величины х в интервал [а,b] равна Эта площадь под кривой плотности вероятности Особое значение имеет нормальное распределение вероятности. Центральная предельная теорема утверждает, что если случайную величину можно представить как сумму большого числа не зависящих друг от друга слагаемых, каждое из которых вносит в сумму незначительный вклад, то эта сумма распределена приблизительно по нормальному закону. Числовые характеристики генеральной совокупности. К числовым характеристикам случайной величины по генеральной совокупности относятся математическое ожидание и теоретическая дисперсия. Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений на вероятность соответствующего исхода. Математически если случайную величину обозначить как х, то ее математическое ожидание будет обозначаться как Предположим, что х может принимать n конкретных значений ( и непрерывной случайной величины: Например для распределения
Математическое ожидание Е(х)=1*0,3+3*0,5*5*0,2=2,8. Математическое ожидание случайной величины называют ее средним по генеральной совокупности и обозначается Свойства 1. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е. Свойства 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если х – случайная переменная и а – константа, то Свойства 3. Математическое ожидание константы есть сама эта величина, т.е. Свойства 4. Свойства 5. Свойства 6. Математическое ожидание биномиального распределения равно произведению числа испытаний n на вероятность появления события в одном испытании p, т.е. Теоретической дисперсией случайной величины х называется математическое ожидание квадрата отклонения х от ее математического ожидания Из определения дисперсии следует другая, более удобная формула ее ывчисления Для дискретной случайной величины Для непрерывной случайной величины Дисперсия является мерой рассеяния случайной величины относительно средней (центра). Например, расчет дисперсии для дискретной случайной величины, приведенной выше имеет вид:
Положительное значение Свойства 1. Дисперсия постоянной равна нулю, т.е. Свойства 2. При умножении случайной величины на константу ее дисперсия умножается на квадрат этой константы Свойства 3. Дисперсия суммы независимых случайных величин равна сумме их дисперсии Свойства 4. Свойства 5. Дисперсия биномиального распределения где n - число независимых испытании; p - вероятность появления события в одном испытании; q=1-p вероятность не появления события в одном испытании. Нормальное распределение случайной величины характеризуется двумя параметрами: средним значением Это обозначается: Нормальное распределение для которого математическое ожидание равно нулю, а дисперсия равна единице называется стандартным нормальным распределением и записывается в виде |
||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 392. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
 ) наносятся на прямоугольную систему координат) и гистограммы (интервал в которую попадают все наблюдения величины
) наносятся на прямоугольную систему координат) и гистограммы (интервал в которую попадают все наблюдения величины  разбивают на несколько промежутков одинаковой длины. Гистограмма – это кусочно-постоянная функция).
разбивают на несколько промежутков одинаковой длины. Гистограмма – это кусочно-постоянная функция).




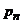
 .
. .
.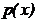 на отрезке a,b . Поскольку какое-либо значение х реализуется, то
на отрезке a,b . Поскольку какое-либо значение х реализуется, то  .
. .
. ) и что вероятность получения
) и что вероятность получения  равна
равна  . Тогда математическое ожидание дискретной случайной величины равна
. Тогда математическое ожидание дискретной случайной величины равна (1)
(1) .
. . Геометрически: математическое ожидание случайной величины – это центр ее распределения.
. Геометрически: математическое ожидание случайной величины – это центр ее распределения. (2)
(2) (3)
(3)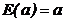 .
. .
. , т.к
, т.к 

 , т.е.
, т.е. (4)
(4)
 ,
, .
. ,
, 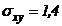 .
. -теоретическое стандартное отклонение, которое вычисляется путем простого извлечения квадратного корня из дисперсии.
-теоретическое стандартное отклонение, которое вычисляется путем простого извлечения квадратного корня из дисперсии. , где
, где  -константа.
-константа. .
. .
.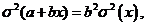 где
где  -постоянные.
-постоянные. ,
, .
.