Для распределений, не являющихся нормальными, предпочтительнее пользоваться ранговыми коэффициентами корреляции Спирмена или Кендалла.

Существуют и другие коэффициенты корреляции, применяющиеся для разных типов данных. Расчёт коэффициента корреляции между двумя недихотомическими переменными не лишён смысла только тогда, кода связь между ними линейна (однонаправлена). Если связь, к примеру, U-образная (неоднозначная), то коэффициент корреляции непригоден для использования в качестве меры силы связи: его значение стремится к нулю.

Метод вычисления коэффициента корреляции зависит от вида шкалы, к которой относятся переменные.

Линейная и криволинейная корреляции

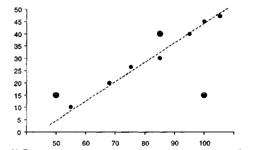
Основной коэффициент корреляции r Пирсона является мерой прямолинейной связи между переменными: его значения достигают максимума, когда точки на графике двумерного рассеяния лежат на одной прямой линии. В реальной жизни отношения между переменными часто оказываются не только вероятностными, но и непрямолинейными; монотонными или немонотонными.

Если связь нелинейная, но монотонная, вместо r Пирсона следует использовать ранговые корреляции Спирмена или Кендалла.

Нередко связь между двумя переменными является не только нелинейной, но и немонотонной.

Например представлены данные о бюджетах 10 партий и о числе полученных этими партиями мест в парламенте, которые графически отображены на диаграмме рассеивания

Между переменными X и Y существует линейное отношение: если одна переменная возрастает по величине, происходит возрастание зависимой переменной и что чем более ком­пактно располагаются точки-наблюдения вокруг пунктирной пря­мой линии (описывающей идеальное линейное отношение X и Y), тем сильнее зависимость.

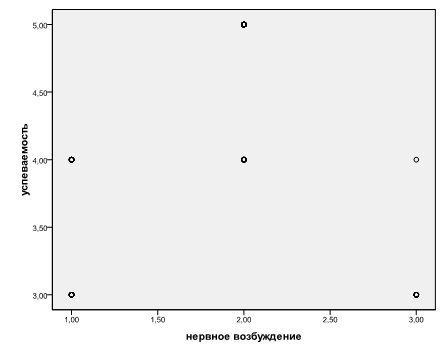
а – отсутствие связи между X и Y

б – обратная (отрицательная) умеренная связь

в – наличие нелинейной связи между переменными.

Пример:ф. Тестирование 1999, переменные «нервное возбуждение перед экзаменом» и «балл экзамена», измеряемые по 3 и 5-бальной шкале соответственно. Студенты, испытывающие умеренное нервное возбуждение, имеют наилучшие результаты на экзаменах, в то время как очень спокойные или очень нервные студенты сдают экзамены значительно хуже. Если по оси абсцисс отложить степень нервного возбуждения, а по оси ординат — результаты сдачи экзаменов, график зависимости между ними примет вид, близкий к перевернутой букве U. При этом любой коэффициент корреляции, вычисленный для этих величин, окажется весьма низким. Это объясняется тем, что для немонотонных отношений нужны другие методы оценки корреляции (регрессионного анализ).