Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Взаимосвязи между линейной регрессией и корреляциейЛинейный коэффициент корреляции
Пример: выявить наличие связи между дневной и ночной температурами в 10 городах мира
Корреляция между дневными и ночными температурами воздуха очень высока полученной величине корреляции. Знание дневных температур позволяет предсказывать ночные температуры с высокой точностью, но не безошибочно. Коэффициент корреляции позволяет оценить степень связи между переменными. Однако этого недостаточно для того, чтобы непосредственно преобразовывать информацию, относящуюся к одной переменной, в оценки другой переменной. Пример: коэффициент корреляции между переменными «величина партийного бюджета» и «число мест в парламенте» равен 0,8. однако, невозможно предсказать, сколько мест в парламенте получит партия, годовой бюджет которой равен 100 млн. рублей. Коэффициент корреляции представляет собой оценку соответствия разброса наблюдений от идеальной модели линейного функционального отношения – прямой линии, называемой линией регрессии. а —значение Y для случая, когда Х = 0 b — коэффициент регрессии, Статистические процедуры позволяют найти регрессионную прямую, максимально соответствующую реальным данным. Регрессионный анализ, таким образом, дает возможность предсказывать значения Y по значениям X с минимальным количеством ошибок  Пример:прогнозирования количества мест от величины партбюджета
Линия регрессии не обязательно должна быть прямой, но нелинейные связи во многих случаях также могут быть приближенно описаны линейными отношениями. Регрессионный анализ в SPSS представляется как диаграмма рассеивания. Выбор коэффициента может быть предварен построением график двумерного рассеяния, который позволит дать наглядное представление о связи двух переменных (п.м. Графика Рассеяние/точки). На графике каждый объект представляет собой точку, координаты которой заданы значениями двух переменных. Таким образом, множество объектов представляет собой на графике множество точек. По конфигурации этого множества точек можно судить о характере связи между двумя переменными.
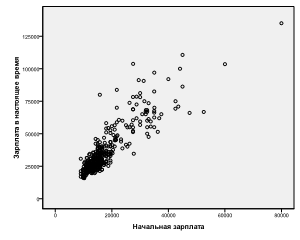
Если все точки-наблюдения размещены на регрессионной прямой – это случай абсолютной линейной зависимости. В этом случае коэффициент корреляции будет равен единице, что свидетельствует о сильном, «абсолютном», характере связи переменных. Различие между предсказанными и наблюдаемыми значениями в этом случае отсутствует. Корреляция как мера точности прогноза показывает, что ошибок в прогнозе не существует. Например: b =313, можно утверждать, что единичная прибавка в величине X вызовет увеличение Y на ту же величину, 313 (если, допустим, X — стаж работы, а Y — зарплата, то с увеличением стажа на год зарплата растет на 313 рублей). В действительности из-завлияния других переменных точки-наблюдения обычно лежат выше или ниже прямой, которая являетсялишь наилучшим приближением реальных данных. Коэффициент корреляции Пирсона r и величина r2 по-прежнему служат оценкой точности прогноза, основанного на линии регрессии. Смысл отношения между корреляцией и регрессией: ¾ корреляция описывает степень «разбросанности» точек наблюдения (чем выше «разбросанность», тем ниже r2 и ненадежнее прогноз) ¾ коэффициент регрессии описывает наклон линии. Для стандартизованных данных коэффициент регрессии коэффициенту корреляции Пирсона. В SPSS расчет коэффициентов корреляции возможен через п.м. Анализ-Корреляции-Парные. В окне Парные корреляции выбрать переменные для вычисления корреляции. В группе Коэффициенты корреляции возможно установление флажков вычисления коэффициентов Пирсона, Спирмена и Тау-b Кендалла, что дает возможность сравнивать эти коэффициентов корреляции для различных распределений данных. В группе Критерий значимости по умолчанию установлен переключатель Двухсторонний. Установить переключатель Односторонний в случае уверенности в направлении (знаке) корреляции. Флажок Метить значимые корреляции по умолчанию установлен. Это означает, что корреляции, вычисленные с уровнем значимости от 0,01 до 0,05, будут помечены одной звездочкой (*), а от 0 до 0,01 — двумя звездочками (**). Вне зависимости от значимости в вывод включаются коэффициенты корреляции и p-уровни, вычисленные с точностью до трех знаков после запятой, а также количество объектов, участвовавших в процедуре. В группе Статистики имеется два флажка, управляющих отображением статистических величин: Средние и стандартные отклонения и Суммы перекрестных произведений отклонений и ковариации. Группа Пропущенные значения из двух переключателей позволяет выбрать способ исключения объектов, содержащих пропущенные значения. Установка переключателя Исключать наблюдения попарно означает, что если при вычислении корреляции между парой переменных для какого-нибудь объекта обнаружится отсутствующее значение, объект будет исключен из вычисления, но только для этой пары переменных. В результате может оказаться, что для разных пар переменных коэффициенты корреляции будут вычислены с разным числом объектов. При установке переключателя Исключать наблюдения целиком программа перед началом вычислительного процесса исключит из рассмотрения все объекты, содержащие хотя бы одно отсутствующее значение. В любом случае разрешение проблемы отсутствующих значений лучше провести до начала анализа. Кн. Параметры позволяет вывести средние значения и квадратные отклонения.
Результаты содержат к. Пирсона, количество использованных пар значений (N) и вероятность ошибки р, соответствующее предположению о ненулевой корреляции. В примере присутствует очень слабая корреляция (0,182) с вероятностью в 0,000. Рассмотрим нормальные независимые случайной величины Xi, дисперсия которой равняется 0, а среднеквадратическое отклонение равно1
Тогда сумма квадратов этих величин Говорят, случайная величина распределена по закону хи-квадрат с степенями свободы k=n-1. С увеличением числа степеней свободы распределение приближается к нормальному. 1. Проверка гипотезы о расхождении между эмпирическими (экспериментальными) частотами ni и теоретическими (контрольными) частотами ni* . |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 494. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
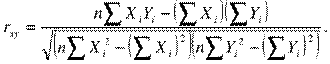
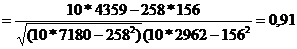
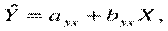
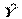 — то предсказываемое значение по переменной Y (например, количество мест в парламенте)
— то предсказываемое значение по переменной Y (например, количество мест в парламенте)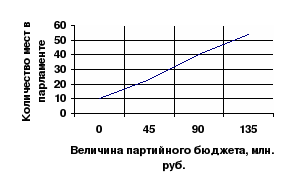
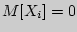 , a
, a 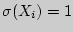 .
.