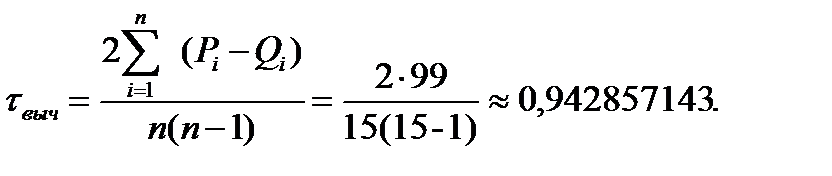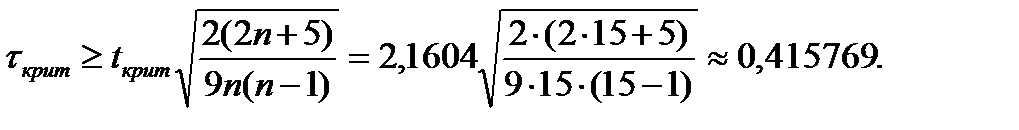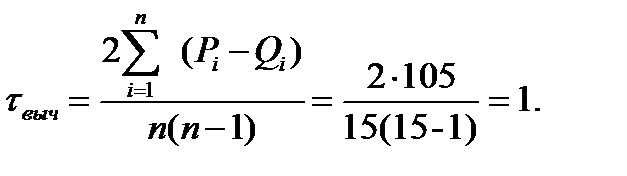Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Коэффициент корреляции рангов КендаллаДля определения тесноты связи, как между количественными, так и между качественными признаками, характеризующие однородные объекты и ранжированные по одному и тому же принципу можно использовать коэффициент корреляции рангов Кендалла, вычисляемый по формуле:
где Рi – количество случаев для i-го варианта, ранг которых превышает i-е значение; Qi - количество случаев для i-го варианта, ранг которых не превышает i-е значение; n - количество вариантов. Существенность коэффициента корреляции рангов Кендалла, при условии нормальности распределений случайных величин, проверяют по формуле:
Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы n-2. Таблица 8.3.1. Сравнение результатов параметра «Среднее время ожидания в очереди» по коэффициенту Кендалла.
Вычисленное значение положительно и превышает рекомендуемое значение 0,50, что указывает на наличие существенной зависимости между переменными.  При допущении о нормальности распределений исходных данныхсущественность коэффициента корреляции рангов Кендалла проверим по формуле: Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2=13: tкрит=2,1604. Так как τвыч > τкрит то делаем заключение о наличии существенной связи между переменными.
Таблица 8.3.2. Сравнение результатов параметра «Среднее время в системе» по коэффициенту Кендалла.
Вычисленное значение положительно и превышает рекомендуемое значение 0,50, что указывает на наличие существенной зависимости между переменными. При допущении о нормальности распределений исходных данныхсущественность коэффициента корреляции рангов Кендалла проверим по формуле: Критическое значение критерия Стьюдента находится по статистическим таблицам для рекомендуемого значения уровня значимости α=0,05 и количества степеней свободы п-2=13: tкрит=2,1604. Так как τвыч > τкрит то делаем заключение о наличии существенной связи между переменными.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 309. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
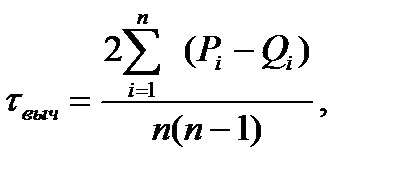 (12)
(12)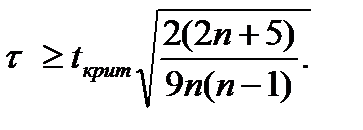 (13)
(13)