Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Методика выполнения задания по курсовой работеСтр 1 из 8Следующая ⇒ Содержание 1.Оценка результатов имитационного моделирования. 3 2.Методика выполнения задания по курсовой работе. 5 3.Стратегическое планирование. 5 4.Значения результатывных показателей эффективности функционирования СМО по аналитической модели по вариантам стратегического плана. 8 5. Разработать и отладить имитационную модель в СИМ GPSS W... 12 6. Имитационное моделирование по вариантам стратегического плана. 14 7. Оценка однородности результатов ИМ с результатами АМ параметрическими методами. 16 8. Корреляционный анализ результатов АМ и ИМ.. 37 9. Выводы.. 84
Задание на курсовую работу №17 Оценка результатов имитационного моделирования (ИМ) системы массового обслуживания (СМО) M/M/m c результатами аналитического моделирования (АМ) 1. Результативные показатели эффективности функционирования СМО приведены в таблице 1. Таблица 1
 2. Диапазоны изменения факторов приведены в таблице 2. Таблица 2
Временные параметры распределены по экспоненциальному закону. 3. Составить стратегический план моделирования, состоящий из 15 вариантов: одной центральной точки, восьми точек плана полного факторного эксперимента (ПФЭ), шести звёздных точек. 4. Вычислить значения результативных показателей эффективности функционпрования СМО по аналитической модели по вариантам стратегического плана. 5. Разработать и отладить имитационную модель в СИМ GPSS W. 6. Провести ИМ СМО в СИМ по вариантам стратегического плана. 7. Оценить однородность результатов ИМ c результатами АМ. Средние значения оценить по разнице в процентах, по доверительному интервалу и по критерию Стьюдента. Дисперсии оценить по критерия Пирсона и Фишера. 8. Провести корреляционный анализ результатов ИМ, с результатами АМ по: коэффициенту Фехнера, ранговому коэффициету корреляции Спирмена, ранговому коэффициету корреляции Кендалла, коэффициенту линейной корреляции, эмпирическому корреляционному отношению. Пункты 7 и 8 выполнить по среднему времени ожидания заявки в очереди и пребывания заявки в системе. 9. Провести анализ полученных результатов и составить отчёт. Профессор кафедры АСОИУ И.М. Якимов 9.02.2017 г. Методика выполнения задания по курсовой работе 1 пункт курсовой работы выполнен в задании на курсовую работу. В таблицу 1 дополнительно введён столбец обозначений результативных показателей эффективности функционирования СМО. 2 пункт курсовой работы в основном выполнен в задании на курсовую работу.В таблицу 2 дополнительно введён столбец обозначений факторов. Требуется составить таблицу 3 соответствия реальных значений факторов ко-дированным, изменяющимся в диапазонах от -1 до +1. Таблица 3
Пункт 3 –стратегическое планирование Стратегический план составляется в соответствии с допущением о виде уравнений регрессии математической модели. Если примем допущение, что уравнения регрессии нелинейные и нелинейность второй степени, то для получения зависимости вида: y = b0x0+b1x1+b2x2+b3х3+b12x1x2+b13x1x3+ b23x2x3 +b123x1x2х3 +b11x12+b22x22+b33х32, (1) Ввиду того, что в уравнение регрессии (1) входит11 переменных, то для их определения требуется провести имитационное моделирование (ИМ) не менее чем по 12 вариантам. При использовании в качестве ядра плана полного факторного эксперимента (ПФЭ) и дополнительного ИМ к нему в центральной точке и в пяти звёздных точках общее количество вариантов составит: N=1+2m+2k=1+23+2∙3=1+8+6=15. (2) Матрица стратегического планирования для 7 факторов в кодированном виде приведена в таблице 4 Таблица 4
Пункт 4 - вычисление значений результативных показателей эффектив-ности функционирования СМО по аналитической модели по вариантам стратегического плана производится по готовым формулам, приведённым в СМО от Кирпичникова.
Модель М/М/m Вычислим значений результативных показателей эффективности функционирования СМО на примере центральной точки, т.е. факторы принимают следующие значения:
1. Вероятность, что в момент поступления заявки СМО свободна
Среднее время между поступлением заявок Среднее время обслуживания одной заявки Количество ОА m =3
Интенсивность поступления транзактов в систему:
Интенсивность обслуживания транзактов в ОА:
Приведённая плотность поступления транзактов в систему:
Вероятность отсутствия транзактов в системе:
Вероятность ожидания:
Среднее количество транзактов в обслуживающих аппаратах:
Среднее количество транзактов в очереди.
Среднее количество транзактов в системе:
Проверка:
Среднее время обслуживания транзактов в ОА:
Среднее время пребывания транзактов в системе:
Среднее время ожидания транзактов в очереди:
Проверка:
Условие выполняется. Дисперсия количества транзактов в ОА:
Стандартное отклонение количества транзактов в ОА:
Дисперсия количестватранзактов в очереди:
Стандартное отклонение количества транзактов в очереди:
Дисперсия количестватранзактов в системе:
Стандартное отклонение количества транзактов в системе:
Дисперсия времени обслуживания транзактов в ОА:
Стандартное отклонение времени обслуживания транзактов в ОА:
Дисперсия времени ожидания транзактов в очереди:
Стандартное отклонение времени ожидания транзактов в очереди:
Дисперсия времени пребывания транзакта в системе:
Стандартное отклонение времени пребывания транзактов в системе:
Ввиду того, что количество транзактов в очереди зависит от количества транзактов на обслуживании требуется эту связь оценить количественно по ковариации:
Отметим, что ковариация времени ожидания и времени обслуживания равна нулю так как эти переменные независимы друг от друга. Должны выполняться следующие равенства:ё
Все вычисления выполнены с помощью Excel.
Основные результаты аналитического моделирования приведены в таблице 5.1 Таблица 5.1 – Основные результаты аналитического моделирования СМО М/М/3
Таблица 5.2. Результаты аналитического моделирования.
Пункт 5. Разработать и отладить модель в СИМ GPSS W Структурная схема системы массового обслуживания с экспоненциальным входным потоком и обслуживанием и с количеством обслуживающих аппаратов, равным m, приведена на рис.5.1.
Здесь требуется привести программную модель на языке GPSS W и отчёт по результатам моделирования первого варианта. Результаты имитационного моделирования по результатам стратегического планирования при прогоне 10000 транзактов для СИМ GPSS W приведены в таблице 6. Пункт 6. Имитационное моделирование по вариантам стратегического плана Таблица 6. Результаты ИМ в GPSS W
Пункт 7.Оценка однородности результатов ИМ, полученных в СИМ Arena с результатами АМ параметрическими методами. Самый простой метод параметрической оценки результатов ИМ – оценка их различия от результатов АМ, выраженное в процентах:
где уij* - оценка i-го параметра, определённая по результатам ИМ для j-го генератора случайных чисел; yi - значение i-го параметра, вычисленное по результатам АМ. Просчитаем параметрическую оценку результатов параметра «Среднеевремя ожидания в очереди» для 1-го варианта для СИМ «Arena» И АМ: Таблица 7.1. Результаты сравнения АМ и ИМ по параметру «Среднее время ожидания в очереди» в процентах.
Результаты сравнения считаются удовлетворительными, если разница ИМ и АМ не превышает 5%. Удовлетворительные оценки для результатов ИМ и АМ получены по 5 тестам из 15, что составляет 33%. Посчитаем среднюю разницу в процентах для параметра «Среднее время ожидания в очереди»: 23,6397818%. Пример расчета параметрической оценки результатов для параметра «Среднее время пребывания в системе» для 1-го варианта для ИМ и АМ: Результаты оценки разности параметра «Среднее время пребывания в системе» для ИМ и АМ для 15 вариантов приведены в таблице 7.2. Таблица 7.2. Результаты сравнения АМ и ИМ по параметру «Среднее время пребывания в системе» в процентах.
Результаты сравнения считаются удовлетворительными, если разница не превышает величину в 5%. Удовлетворительные оценки по параметру «Среднее время пребывания в системе» получено по 14 тестам из 15. Посчитаем среднюю разницу в процентах для параметра «Среднее время пребывания в системе»: 1,264640822%. Полученные результаты будем считать удовлетворительными. По показателю «Среднее время пребывания в системе» получены лучшие результаты, примерно меньше в 10 раз, чем результаты по параметру «Среднее время ожидания в очереди». Это связано с тем, что результаты параметра «Среднее время ожидания в очереди» в основном составляют сотые части от единицы. Из-за столько малых величин различие даже на сотую часть покажет отличие в несколько процентов. В то время, как результаты параметра «Среднее время пребывания в системе» варьируются в интервале от 10 до 60 и различие в несколько сотых долей покажет несущественную разницу в процентах. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 287. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
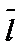
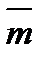
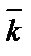
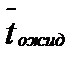
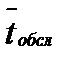
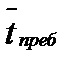
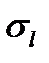
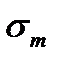
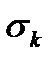
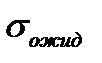
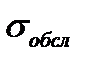
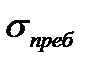
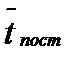
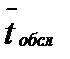
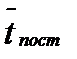 =100
=100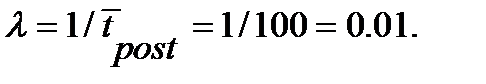
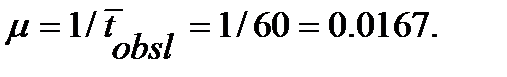
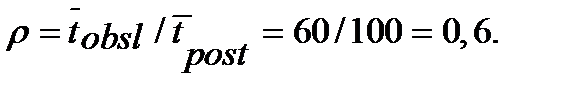
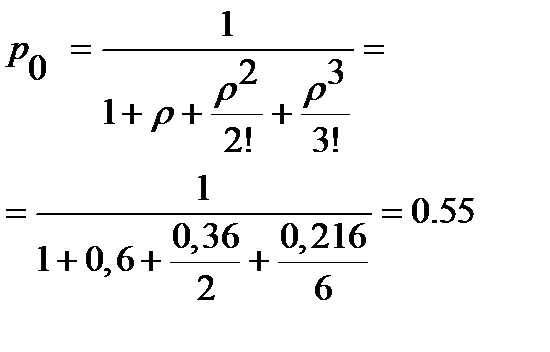
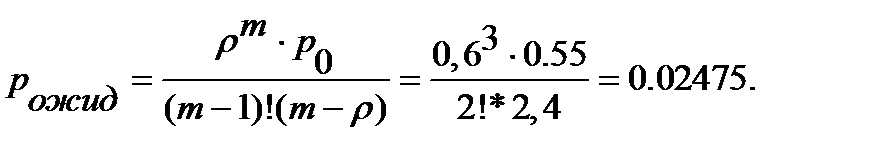
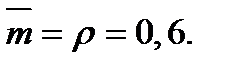
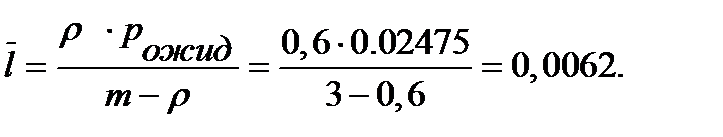
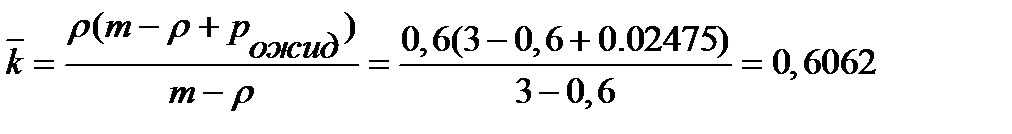
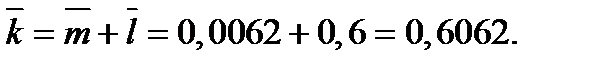
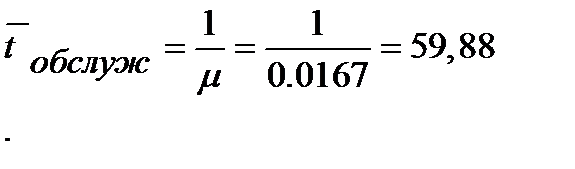
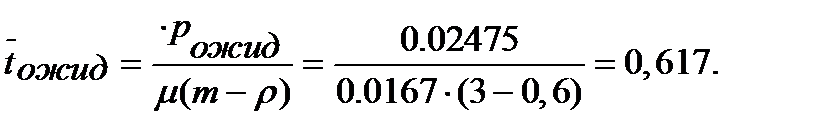
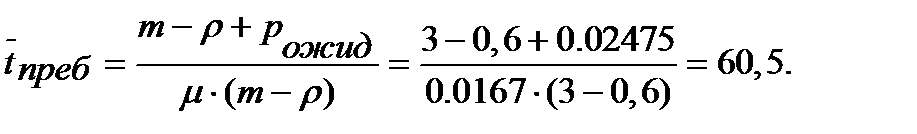
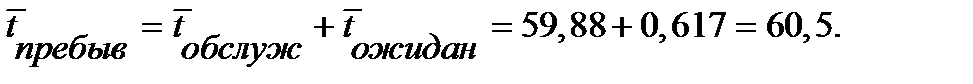
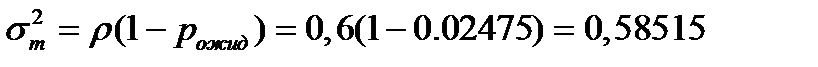 .
.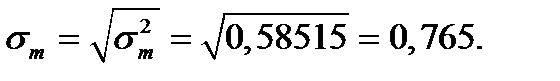
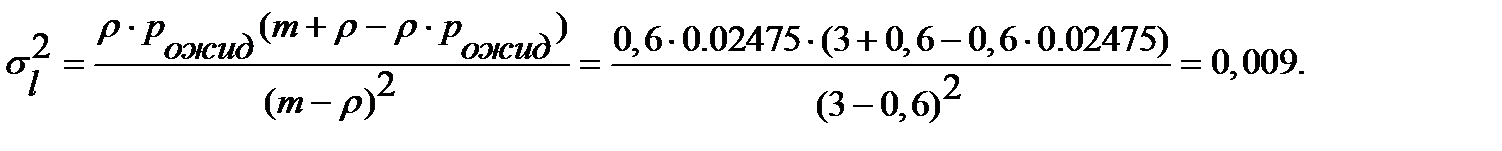
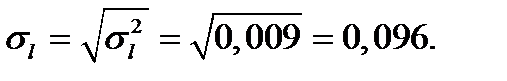 .
. 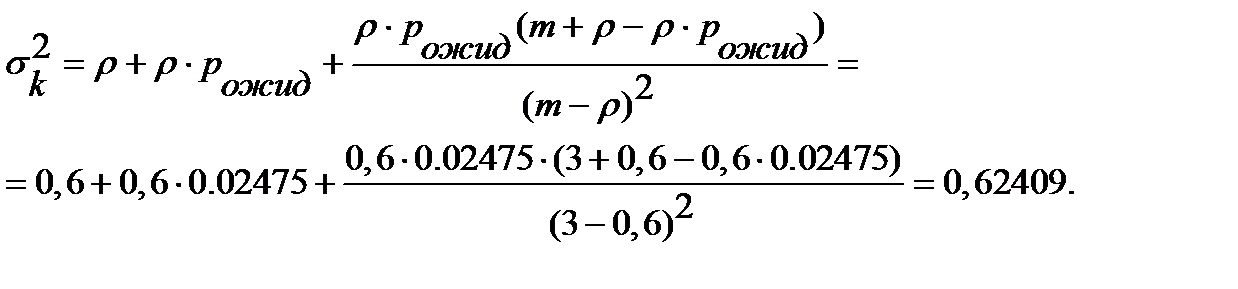
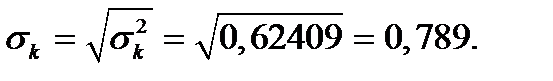
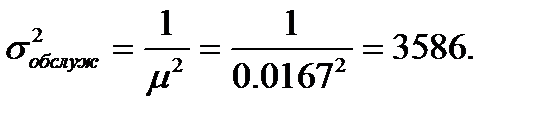
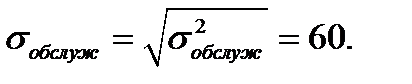
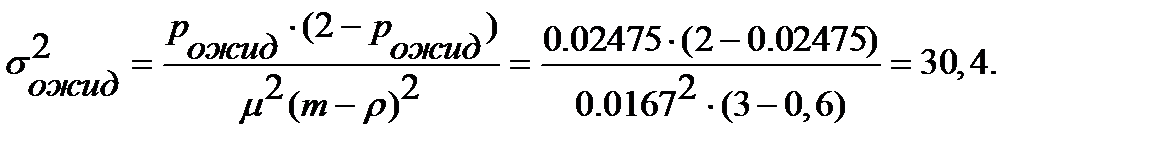
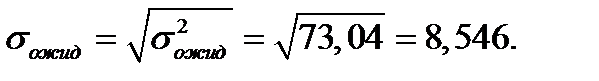
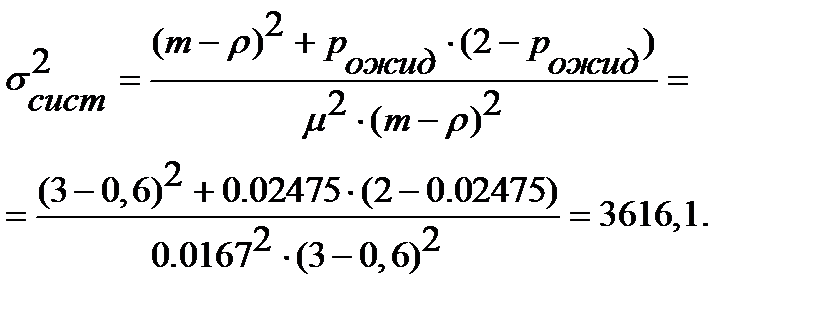 .
.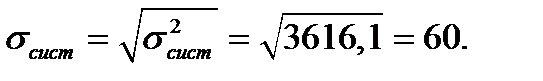
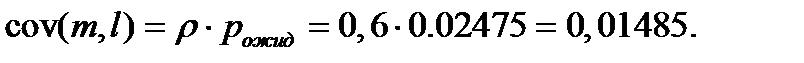
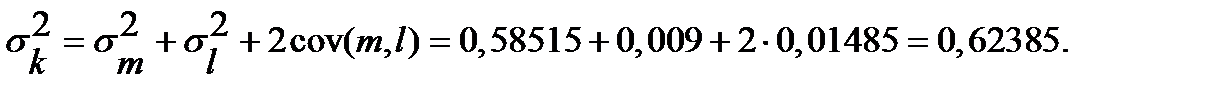
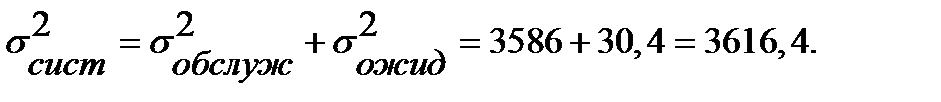
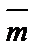
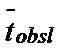
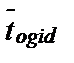
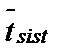
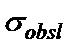
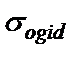
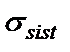
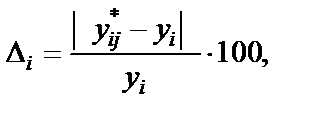 (1)
(1)