Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Векторы и прямые произведения множеств.Проекция вектора на ось Вектор – это упорядоченный набор элементов (“кортеж”). Его элементы зазываются координатами или компонентами вектора. Длина (размерность) вектора – число координат вектора. В отличие от элементов множества, его координаты могут совпадать. Обозначение вектора: в круглых скобках, координаты – через запятую (0, 5, 4, 5, 0, 1). Иногда скобки и даже запятые опускаются. Векторы длины 2 называют упорядоченными парами; длины 3 – тройками; и т.д., длины n – n-ками. Два вектора равны, если они имеют одинаковую длину, и соответствующие координаты равны, т. е. Прямое произведение n множеств
Пусть А – конечное множество, элементами которого являются символы (буквы, цифры, знаки препинания, знаки операций и т. д.). Такие множества обычно называют алфавитом. Слова длины n в алфавите А – это элементы множества
Здесь слово определено как вектор. При написании слова не принято пользоваться разделителями: скобками, запятыми; они могут оказаться символами самого алфавита. Поэтому слово в алфавите обозначается как конечная последовательность символов из алфавита А. Примеры: 1) Десятичное число – слово в алфавите цифр {0, 1, 2, 3, ... , 9}. 2) Текст, отпечатанный на машинке – слово в алфавите, определяемом клавиатурой этой машинки. Теорема (о мощности прямого произведения множеств). Пусть
Следствие: Эта теорема и ее следствие лежат в основе очень многих комбинаторных фактов.  Проекцией вектора Проекцией вектора Пусть V – множество векторов одинаковой длины. Проекцией множества векторов V на i-ось называется множество проекций всех векторов из V на i-ось: (обозначение: Проекция множества векторов V на оси с номерами
В частности, если В общем случае Примеры: 1) Проекция точки плоскости на 1-ю ось – абсцисса, на 2-ю ось – ордината. 2) Дано множество векторов
3)
УПРАЖНЕНИЯ 1. Пусть
2. Определить мощности множеств 1) 2)
3. Записать все слова из 3-х букв, которые можно построить из алфавита А. Осуществить перечисление в лексикографическом порядке. 1) 4. Пусть 1) 2)
5. Найти 1) 2) 3) 4) 1.3.Комбинаторика Правило суммы Классическая формулировка Если элемент Современная формулировка(теорема о мощности объединения множеств) Количество элементов объединения двух множеств равно сумме количества элементов в первом и во втором множестве, за вычетом количества элементов их пересечения:
Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке:
Для трех множеств теорема имеет вид:
Общее правило для
Правило произведения Классическая формулировка Если элемент Современная формулировка(теорема о мощности прямого произведения множеств) Количество элементов прямого произведения двух множеств равно произведению количества элементов первого и второго множества:
Пример. Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 6 экземпляров учебника физики, надо выбрать комплект, содержащий все учебники по одному разу. Сколькими способами это можно сделать? Множество А – учебники по алгебре, В – учебники по геометрии, С – по физике. Надо составить и пересчитать все тройки из множества |
||||||||||||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 295. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
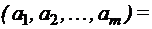
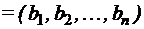 , если
, если 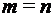 и
и  ,
, 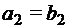 , …,
, …, 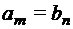 .
.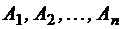 (обозначается
(обозначается 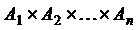 ) называется множеством всех векторов
) называется множеством всех векторов 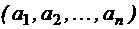 , длины n таких, что
, длины n таких, что 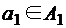 ,
, 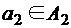 , ...,
, ..., 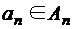 .
.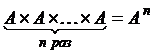 .
. . Множество всех слов в алфавите А – это множество
. Множество всех слов в алфавите А – это множество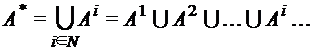
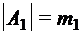 ,
, 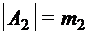 , ... ,
, ... , 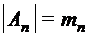 . Тогда мощность множества
. Тогда мощность множества  равна произведению мощностей множеств
равна произведению мощностей множеств 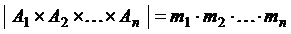 .
.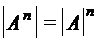 .
.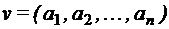 длины n на i-ю ось называется его i-я координата (обозначение: )
длины n на i-ю ось называется его i-я координата (обозначение: ) 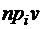 .
.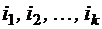 называется вектор
называется вектор 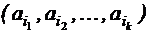 длины k (обозначение:
длины k (обозначение: 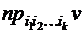 ).
).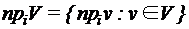 .
.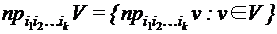 .
. , то
, то 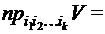 =
= 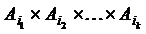 .
.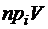 - вовсе не обязательно прямое произведение, оно может быть и подмножеством.
- вовсе не обязательно прямое произведение, оно может быть и подмножеством. ;
;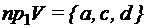 ,
,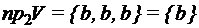 ,
,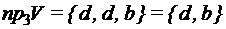 ,
,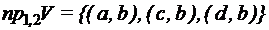 ,
, 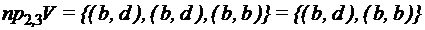 ,
, .
.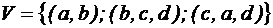 . Чему равна
. Чему равна 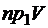 ? Ее найти нельзя, так как заданное множество V- множество векторов разной длины, в отношении которых никаких определений не было сделано.
? Ее найти нельзя, так как заданное множество V- множество векторов разной длины, в отношении которых никаких определений не было сделано.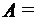 {2, 3};
{2, 3}; 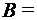 {3, 4};
{3, 4}; 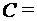 {1, 0}. Найти:
{1, 0}. Найти: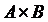 ;
;
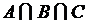 ;
;
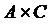 ;
;
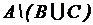 ;
;
 ;
;
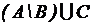 ;
;
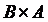 ;
;
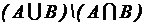 ;
;
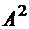 ;
;
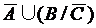 .
.
 ;
; 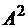 ;
; 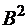 ;
;  ;
;  , и построить их, если
, и построить их, если  ;
; 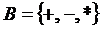 ; 3)
; 3) 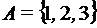 ;
; 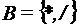 ;
; = {(1; 2)},
= {(1; 2)},  = {a; b; c; d}; 4)
= {a; b; c; d}; 4) 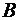 = {1; 2}.
= {1; 2}.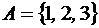 ; 2)
; 2) 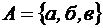 ; 3)
; 3) 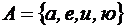
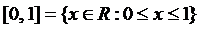 ;
; 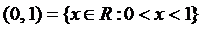 ;
; 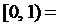
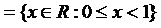 и
и  . Описать и изобразить графически следующие множества
. Описать и изобразить графически следующие множества 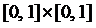 ; 3)
; 3) 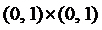 ;
;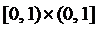 ; 4)
; 4) 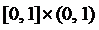
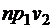 ;
; 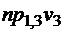 ;
; 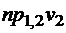 ;
; 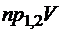 ;
; 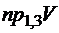 , если
, если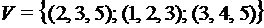 ;
;  ;
;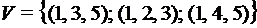 ;
; 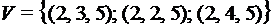 .
.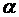 можно выбрать k способами, а элемент
можно выбрать k способами, а элемент  можно выбрать m способами. Тогда
можно выбрать m способами. Тогда 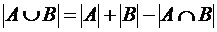 .
.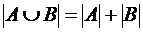 .
.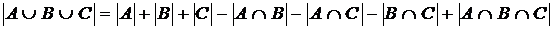 .
. имеет вид::
имеет вид::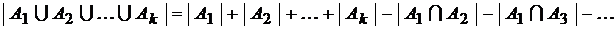

 можно выбрать k способами, а элемент
можно выбрать k способами, а элемент 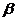 можно выбрать m способами. Тогда
можно выбрать m способами. Тогда 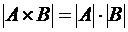 .
.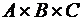 .
.