
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Относительных(P) величин по критерию t.В медицинских исследованиях часто возникает необходимость оценивать показатели, выраженные как средними, так и относительными величинами, которые получены в разных статистических совокупностях. При этом требуется не только определить различие (разность) сравниваемых показателей, но и определить его достоверность. Последняя оценивается с помощью доверительного критерия (или критерия точности) t. О наличии или отсутствии достоверных различий между сравниваемыми величинами судят по размеру получаемого критерия t. Если критерий t равен 2, различие достоверно и это можно утверждать с вероятностью безошибочного прогноза, равной 95 % (при t = 3 и более - с вероятностью безошибочного прогноза - 99 %). Величина критерия менее 2 свидетельствует о недостоверном различии сравниваемых показателей. Формула оценки достоверности разности сравниваемых средних величин такова: t= и для относительных величин: t= где M1,M2, P1, P2 – параметры, полученные при выборочных исследованиях; m1 и m2 – их средние ошибки; t – критерий точности. Разность достоверна при t Для большинства исследований, проводимых в медицине и здравоохранении, такая степень вероятности является вполне достаточной.
50. Оценка достоверности различия сравниваемых групп по критерию соответствия χ2 (хи – квадрат). Определяя с помощью X2(хи-квадрат) соответствие эмпирического распределения теоретическому оценивают достоверность различия между выборочными совокупностями. Критерий X2 (в отличие от критерия t) применяется в тех случаях, когда нет необходимости знать величину того или иного параметра (среднюю или относительный показатель) и требуется оценить достоверность различия не только двух, но и большего числа групп Х2  Так, критерий X2(хи-квадрат) может быть использован для ответа на следующие вопросы: существенно ли отличаются друг от друга группы вакцинированных и невакцинированных по распределению их на больных и здоровых (т. е. эффективна ли вакцина); существенно ли отличаются группы населения с разным среднедушевым доходом по распределению их на больных и здоровых (т. е. влияет ли материальное обеспечение на уровень заболеваемости) и т. п. Критерий X2(хи-квадрат) определяется по формуле: X2= Где «Нулевая гипотеза» - это предположение о том, что в сравниваемых группах отсутствует различие в распределении частот. Например, допускается одинаковое распределение больных и здоровых в группах вакцинированных и невакцинированных. Определение критерия соответствия X2 основано на расчете разницы между фактическими и ожидаемыми данными. Чем больше это разность (φ – φ1), тем с большей вероятностью можно утверждать, что существуют различия в распределении сравниваемых выборочных совокупностей и, наоборот, чем меньше разность (φ – φ1), тем меньше шансов на то, что сравниваемые выборочные совокупности различны между собой.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 573. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
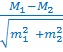 ,
,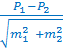 ,
, 2, что соответствует вероятности безошибочного прогноза, равной 95 % и более (P ≥ 95 %).
2, что соответствует вероятности безошибочного прогноза, равной 95 % и более (P ≥ 95 %).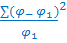 ,
,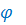 (фи) – фактические (эмпирические) данные,
(фи) – фактические (эмпирические) данные, 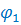 - «ожидаемые» (теоретические) данные, вычисленные на основании нулевой гипотезы (H0).
- «ожидаемые» (теоретические) данные, вычисленные на основании нулевой гипотезы (H0).