Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Здравоохранении. Способы расчета средней арифметической.Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. Наиболее часто в характеристике вариационного ряда используют среднюю арифметическую. Различают три вида средней арифметической: простая, взвешенная и вычисленная по способу моментов. Средняя арифметическая, которая рассчитана в вариационном ряду, где каждая варианта встречается только 1 раз называется средней арифметической простой. Ее определяют по формуле: M= где М – средняя арифметическая, V – варианта изучаемого признака, n–число наблюдений. Если в исследуемом ряду одна или несколько вариант повторяются несколько раз, то вычисляют среднюю арифметическую взвешенную, когда учитывается вес каждой варианты в зависимости от частоты ее встречаемости. Расчет такой средней проводят по формуле: M= где М – средняя арифметическая взвешенная; ∑ - знак суммы; V – варианты (числовые значения изучаемого признака); P – частота, с которой встречается одна и та же варианта признака, т.е. сумма вариант с данным значением признака; n – число наблюдений, т.е., сумма всех частот или общее число всех вариант (∑p). В случаях, когда варианты представлены большими числами (например, масса тела новорожденных в граммах) и имеется число наблюдений, выраженное сотнями или тысячами случаев, взвешенная средняя арифметическая может быть вычислена по способу моментов по формуле: M = A + где A – условно взятая средняя величина (чаще всего в качестве условной средней берется Мо); ∑ - знак суммы; α – отклонение каждой варианты в интервалах от условной средней  p – частота (число раз, с которым встречается одна и та же варианта признака). αp – произведение отклонения (α) на частоту (p); n – число наблюдений, т.е. сумма всех частот или общее число всех вариант (∑p); i – величина интервала. Средняя арифметическая (средняя взвешенная) имеет ряд свойств, которые используют в некоторых случаях для упрощения расчета средней и получения ориентировочной величины. 1. Средняя арифметическая занимает срединное положение в строго симметричном вариационном ряду. 2. Средняя арифметическая имеет абстрактный характер и является обобщающей величиной, выявляющей закономерность. 3. Алгебраическая сумма отклонений всех вариант от средней равна нулю: ∑ (V - M) = 0. На этом свойстве основан расчет средней по способу моментов.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 575. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
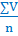 ,
,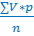 ,
,