
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Характеристика разнообразия признака в статистическойсовокупности Основными критериями разнообразия признака в статистической совокупности являются: лимит, амплитуда, среднее квадратическое отклонение и коэффициент вариации.Средние величины дают лишь обобщающую характеристику изучаемого признака в совокупности и не учитывают значения отдельных его вариант - минимальное и максимальное, выше среднего, ниже среднего и т. д. Определение перечисленных критериев разнообразия признака, прежде всего, осуществляется с учетом его значения у отдельных элементов статистической совокупности. Лимит (lim)- это критерий, который определяется крайними значениями вариант в вариационном ряду. Другими словами данный критерий ограничивается минимальной и максимальной величинами признака: lim = vmin -:- vmax Амплитуда (Am) -это разность крайних вариант.Расчет данного критерия осуществляется путем вычитания из максимального значения признака - его минимального значения, что позволяет оценить степень разброса вариант: Am = vmax - vmin Наиболее полную характеристику разнообразия признака в статистической совокупности дает среднее квадратическое отклонение δ, которое является общей мерой отклонения вариант от своей средней. Расчет среднего квадратического отклонения осуществляется в определенной последовательности и включает пять этапов: 1. Определение средней арифметической (М). 2. Расчет истинного отклонения (d) каждой варианты от средней величины (V - M). 3. Возведение каждого отклонения в квадрат (d2) (если в исследуемой совокупности некоторые варианты встречаются неоднократно (р>1), следующим шагом необходимо умножить размер отклонения этих вариант, возведенного в квадрат (d2), на их частоту (р).  4. Определение суммы (∑ d2 или ∑d2р) 5. Расчет среднего квадратического отклонения (по формулеσ = Коэффициент вариации (Сv)является относительной мерой разнообразия признака в статистической совокупности, поскольку исчисляется как процентное отношение среднего квадратического отклонения (δ) к средней арифметической величине (М). Расчет коэффициента вариации производится по формуле: δ х 100 М Полученное значение оценивается в соответствии с ориентировочными градациями степени разнообразия признака: - слабое — до 10 % - среднее — 10 - 20 % - сильное — более 20 % Использование коэффициента вариации целесообразно в случаях, когда приходится сравнивать признаки разные по своей величине и размерности.
Оценка достоверности результатов исследования.
Под достоверностью статистических данных понимают степень их соответствия отображаемой действительности, т.е. достоверными данными считаются те, которые не искажают и правильно отражают объективную реальность. Оценить достоверность результатов исследования означает определить, с какой вероятностью возможно перенести результаты, полученные на выборочной совокупности, на всю генеральную совокупность. Исходя из этого, оценка достоверности необходима для того, чтобы по части явления можно было судить о явлении в целом и его закономерностях. Оценка достоверности результатов исследования складывается из определения: · ошибок репрезентативности (ошибок средних и относительных величин) - m; ·доверительных границ средних (или относительных) величин; ·достоверности разности (различия) средних (или относительных) величин по критерию t. От степени разнообразия признаков в изучаемой (выборочной) совокупности во многом зависит их репрезентативность по отношению к признакам единиц наблюдения в генеральнойсовокупности. Репрезентативность признаков в виде средних величин характеризуется размером их ошибок (ошибка средней арифметической величины (mM), зависящим от размера среднего квадратического отклонения.
|
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 871. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
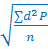 ).
).