
Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Определение средней ошибки средней (или относительной) величины(ошибки репрезентативности) – m.Ошибка репрезентативности является важнейшей статистической величиной необходимой для оценки достоверности результатов исследования. Ошибки репрезентативности возникают всегда, когда требуется по части явления охарактеризовать целое. Эти ошибки неизбежны. Они проистекают из сущности выборочного исследования: генеральная совокупность может быть охарактеризована по одной своей части только с некоторой погрешностью, измеряемой ошибкой репрезентативности. По величине ошибки репрезентативности определяют, насколько результаты, полученные при выборочном наблюдении, отличаются от результатов, которые могли бы быть получены при проведении сплошного исследования всех без исключения элементов генеральной совокупности. Это единственный вид ошибок, учитываемых статистическими методами, которые не могут быть устранены (за исключением перехода на сплошное изучение). Средняя арифметическая величина (выборочной совокупности имеет ошибку репрезентативности, которая называется средней ошибкой средней арифметической (mM) и определяется по формуле: mM= Относительные величины полученные при выборочном исследовании, имеют свою ошибку репрезентативности, которая называется средней ошибкой относительной величины P и обозначается (m% илиm‰соответственно показателю). Определяется по формуле: m% = где P – показатель выраженный в процентах;
Определение доверительных границ M и P. Для оценки достоверности относительных величин (Р), также как и для средних, необходимо рассчитывать их ошибку (mP). Ошибки средних и относительных показателей являются именными величинами, т. е. имеют ту же размерность, что и сами показатели. Наличие ошибки показателей позволяет не только определить их достоверность, но и дает возможность рассчитать их доверительные границы, а также достоверность разности (различия) сравниваемых величин.  Определение доверительных границ средних и относительных величин позволяет найти два их крайних значения - минимально возможное и максимально возможное, в пределах которых изучаемый показатель может встречаться во всей генеральной совокупности. Исходя из этого, доверительные границы (или доверительный интервал) - это границы средних или относительных величин, выход за пределы которых вследствие случайных колебаний имеет незначительную вероятность. Доверительные границы средней арифметической величины в генеральной совокупности определяют по формуле: Мген.= Мвыб. ±tmM для относительной величины: Рген. = Рвыб. ± tmР где Мген. и Рген - значения средней и относительной величины для генеральной совокупности; Мвыб. и Рвыб. - значения средней и относительной величины, полученные на выборочной совокупности; mMи mP - ошибки средней и относительной величин; t - доверительный критерий (критерий точности, который устанавливается при планировании исследования и может быть равен 2 или 3); tm - это доверительный интервал или Δ предельная ошибка показателя, полученного при выборочном исследовании.
Определение достоверности разности средних (M) и |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 605. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
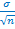
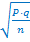
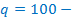 p (при P в промилляхq = 1000- p и т.д.).
p (при P в промилляхq = 1000- p и т.д.).