Студопедия КАТЕГОРИИ: АвтоАвтоматизацияАрхитектураАстрономияАудитБиологияБухгалтерияВоенное делоГенетикаГеографияГеологияГосударствоДомЖурналистика и СМИИзобретательствоИностранные языкиИнформатикаИскусствоИсторияКомпьютерыКулинарияКультураЛексикологияЛитератураЛогикаМаркетингМатематикаМашиностроениеМедицинаМенеджментМеталлы и СваркаМеханикаМузыкаНаселениеОбразованиеОхрана безопасности жизниОхрана ТрудаПедагогикаПолитикаПравоПриборостроениеПрограммированиеПроизводствоПромышленностьПсихологияРадиоРегилияСвязьСоциологияСпортСтандартизацияСтроительствоТехнологииТорговляТуризмФизикаФизиологияФилософияФинансыХимияХозяйствоЦеннообразованиеЧерчениеЭкологияЭконометрикаЭкономикаЭлектроникаЮриспунденкция |
Ихприменение в здравоохранении.Для вычисление коэффициента корреляции используют методы рангов, или метод Спирмена (ρ), квадратов, или метод Пирсона (r), корреляционной решетки (η) и множественной корреляции. Наиболее простым методом является вычисление коэффициента корреляции методом рангов (метод Спирмена), но полученный метод дает приближенные результаты. Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется фактическая степень параллелизма между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента. Коэффициент ранговой корреляции целесообразно применять: - при наличии небольшого количества наблюдении, - когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных, - когда признаки представлены не только количественными, но и атрибутивными значениями, - когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года, 20 лет и более и др.). Мощность коэффициента ранговой корреляции Спирмена несколько уступает мощности параметрического коэффициента корреляции. Наиболее точным и часто применяемым является метод квадратов, или метод Пирсона. Метод квадратов (метод Пирсона) применяется: · когда требуется точное установление силы связи между признаками; · когда признаки имеют только количественное выражение. Достоверность коэффициента корреляции определяется величиной ошибки и доверительным коэффициентом t. В том случае, если полученный коэффициент корреляции в 3 раза и более превышает свою ошибку, он считается достоверным. 
Вычисление ошибки коэффициента корреляции. 1. Ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):
где mp– средняя ошибка коэффициента корреляции, вычисленного методом рангов; ρ – величина коэффициента корреляции, вычисленного методом рангов; n – число наблюдений. 2. Ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):
где mr– ошибка коэффициента корреляции, вычисленного методом квадратов; n – число наблюдений. Оценка достоверности коэффициента корреляции, полученного методом ранговой корреляции и методом квадратов Способ 1. Достоверность определяется по формуле:
Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности ρ ≥ 99%. Способ 2. Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза ρ ≥ 95%.
Стандартизация, понятие. Методы вычисления стандартизованных |
||
|
Последнее изменение этой страницы: 2018-04-12; просмотров: 576. stydopedya.ru не претендует на авторское право материалов, которые вылажены, но предоставляет бесплатный доступ к ним. В случае нарушения авторского права или персональных данных напишите сюда... |
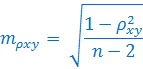
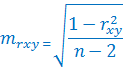
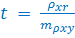 или
или